문제 링크
1238번: 파티
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명


접근 방법
이 문제에 핵심
1. 도로는 단방향으로 이루어집니다.
2. 지역들을 연결하는 중복되는 도로가 존재하지 않습니다.
3. N명의 학생 중 파티에 갔다가 집으로 돌아오는 최대 시간을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 다익스트라를 통해서 각 지역에서 다른 지역으로 이동하는 최단 거리를 모두 탐색합니다.
3. 학생 중 소요시간 최대값을 결과로 출력합니다.
각 지역 최단 거리 탐색!
다익스트라 알고리즘을 통해서 각 지역에서 다른 지역으로 이동하는 최단 거리를 구합니다.
모든 최단 거리를 distnace[][]에 저장한 뒤
소요 시간 : distance[학생 번호][파티 위치] + distance[파티위치][학생번호]
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 4
M : 8
X : 2

2. 다익스트라를 통해서 각 지역에서 다른 지역으로 이동하는 최단 거리를 모두 탐색합니다.
시작 지역 1번일 때!
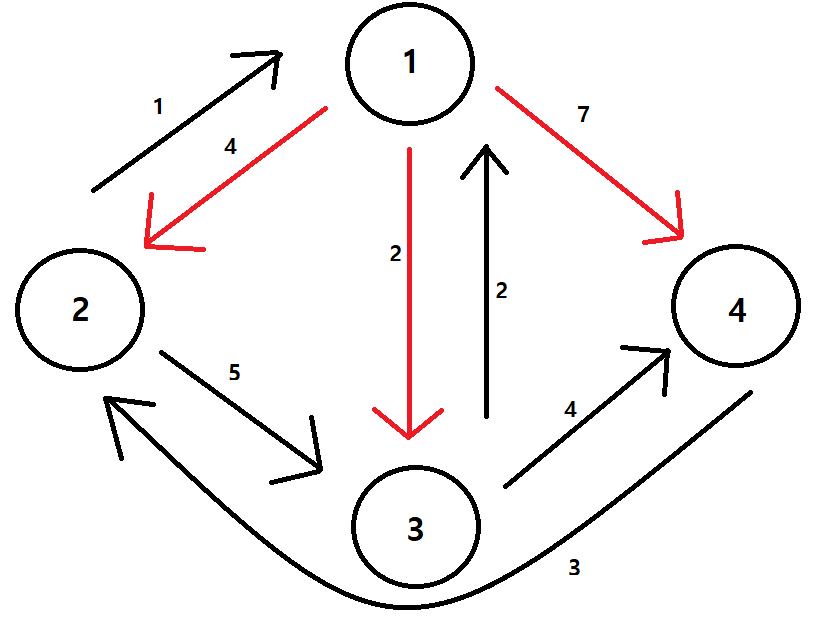
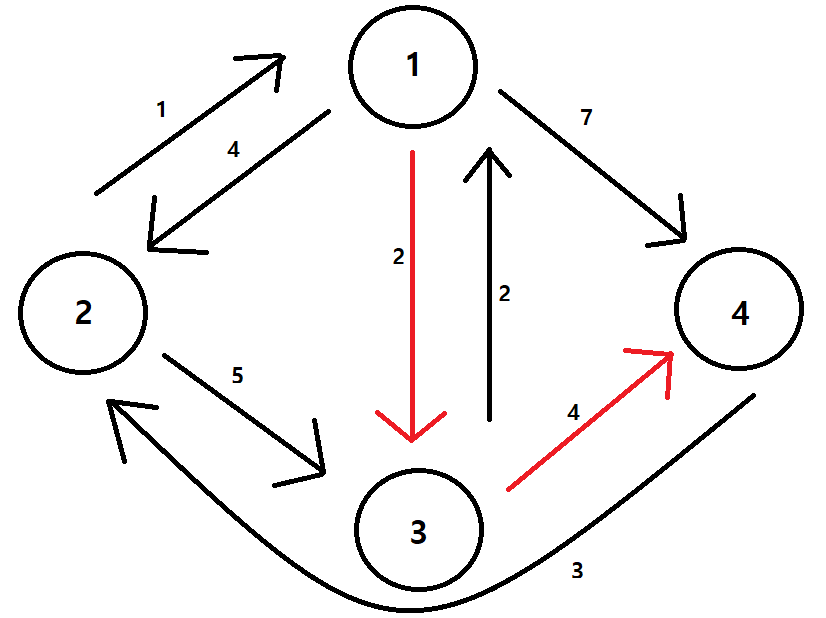
.....
| 지역 1 | 지역 2 | 지역 3 | 지역 4 | |
| 지역 1 | 0 | 4 | 2 | 6 |
| 지역 2 | 1 | 0 | 3 | 7 |
| 지역 3 | 2 | 6 | 0 | 4 |
| 지역 4 | 4 | 3 | 6 | 0 |
3. 학생 중 소요시간 최대값을 결과로 출력합니다.
학생 1번 소요 시간 : distance[1][2] + distance[2][1] = 4 + 1 = 5
학생 2번 소요 시간 : distance[2][2] + distance[2][2] = 0 + 0 = 0
학생 3번 소요 시간 : distance[3][2] + distance[2][3] = 6 + 3 = 9
학생 4번 소요 시간 : distance[4][2] + distance[2][4] = 3 + 7 = 10
10 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 도로의 정보를 띄어쓰기 기준 나누었습니다.
- bfs함수를 이용해서 각 지역에서 시작하는 최단 거리를 distance[][]에 저장합니다.
- 점화식을 통해서 학생 중 최대 소요 시간을 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- bfs함수는 다익스트라 알고리즘을 이용하여 최단 거리를 계산합니다.
결과코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
//길 정보 관련 클래스
static class node implements Comparable<node>{
int position, value;
//position : 지역 위치, value : 소요 시간
public node(int position, int value){
this.position = position;
this.value = value;
}
//소요 시간 오름차순 정렬
@Override
public int compareTo(node o) {
return this.value - o.value;
}
}
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
ArrayList<ArrayList<node>> graph = new ArrayList<>();
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int X = Integer.parseInt(st.nextToken());
int[][] distance = new int[N+1][N+1];
//그래프 초기화 및 거리 초기화
for(int i=0;i<=N;i++) {
graph.add(new ArrayList<>());
Arrays.fill(distance[i], Integer.MAX_VALUE);
}
//도로 정보 저장
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine()," ");
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken());
graph.get(A).add(new node(B, T));
}
int answer = Integer.MIN_VALUE;
//각 지역을 기준 최단 거리 구하기!
for(int i=1;i<=N;i++)
bfs(i, distance, graph);
//최대 소요시간 구하기
for(int i=1;i<=N;i++){
int d = distance[i][X] + distance[X][i]; //소요시간 점화식
answer = Math.max(answer, d); //최대값인지 확인
}
bw.write(String.valueOf(answer)); //최대값 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//다익스트라로 시작 구역에서 다른 지역에 가는 최단 거리를 구하는 함수입니다.
static void bfs(int start, int[][] distance, ArrayList<ArrayList<node>> graph){
PriorityQueue<node> pq = new PriorityQueue<>();
pq.add(new node(start, 0)); //시작 위치 저장
distance[start][start] = 0; //시작 지역 초기 위치 저장
//최단 거리 탐색
while(!pq.isEmpty()){
node cur = pq.poll();
for(node next : graph.get(cur.position)){
int tempValue = cur.value + next.value;
//이동하려는 지역이 최단 거리일 때
if(distance[start][next.position] > tempValue){
distance[start][next.position] = tempValue;
pq.add(new node(next.position, tempValue));
}
}
}
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(브루트포스 알고리즘,JAVA)2502번, 떡 먹는 호랑이 (0) | 2023.01.30 |
|---|---|
| [백준] 알고리즘 분류(자료구조,JAVA)1918번, 후위 표기식 (0) | 2023.01.29 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)1865번, 웜홀 (0) | 2023.01.29 |
| [백준] 알고리즘 분류(수학,JAVA)13172번, Σ (0) | 2023.01.26 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)14938번, 서강그라운드 (2) | 2023.01.25 |




댓글