문제 링크
17404번: RGB거리 2
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명


접근 방법
이 문제에 핵심
1. 건물을 색칠할 때 +1, -1 건물과는 동일한 색으로 칠하지 못합니다.
2. 1번째와 N번재 건물은 동일한 색으로 칠할 수 없습니다.
3. 각 건물을 RGB 색으로 칠할 때마다 발생하는 비용이 존재합니다.
4. 조건에 맞게 모든 건물을 색칠할 때 최소 비용을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 첫 번째 건물의 색에 따른 마지막 건물부터 DP[][]를 구성하여 탐색합니다.
3. 탐색이 끝나고 얻은 유지비의 최소값을 결과로 출력합니다.
첫 번째 건물의 색에 따른 DP탐색!
건물을 색칠할 때 취하는 행동 3가지 경우
1. R색칠하기! (뒷 건물을 R로 칠한 경우 불가능!)
2. G색칠하기! (뒷 건물을 G로 칠한 경우 불가능!)
3. B색칠하기! (뒷 건물을 B로 칠한 경우 불가능!)
Top-Down 방식의 탐색과정!
DP[N][3] 배열을 통해서 각 경우의 최대값을 저장합니다.
DP[i][0] : i번째 열에서 1번 행동(R색칠하기! )를 진행했을 때 최소값
DP[i][1] : i번째 열에서 2번 행동(G색칠하기! )를 진행했을 때 최소값
DP[i][2] : i번째 열에서 3번 행동(B색칠하기! )를 진행했을 때 최소값
DP[][] 초기화 값!
각 첫 번째 건물의 색에 따라 DP[N-1]의 값을 다르게 초기화해주어야 합니다.
첫 번째 건물이 R인 경우
마지막 건물은 R으로 칠할 수 없기 때문에 DP[N-1][0] = 1000001
첫 번째 건물이 G인 경우
마지막 건물은 R으로 칠할 수 없기 때문에 DP[N-1][1] = 1000001
첫 번째 건물이 B인 경우
마지막 건물은 R으로 칠할 수 없기 때문에 DP[N-1][2] = 1000001
※1000001의 값은 문제의 입력값 범위에서 나올 수 없는 값입니다.
DP[][] 계산 점화식!
DP[i][0] : Math.min(DP[i+1][1], DP[i+1][2]) + i번째 R색칠 비용
해석 :
색깔 R을 사용하려면, 뒷 건물이 G, B로 칠해져야 진행해야합니다.
그래서 앞 건물이 G와 B번 칠해진 값 중 작은 값에 현재 R색칠 비용 더한 값이 최소값입니다.
DP[i][1] : Math.min(DP[i+1][0], DP[i+1][2]) + i번째 B색칠 비용
해석 :
색깔 G을 사용하려면, 뒷 건물이 R, B로 칠해져야 진행해야합니다.
그래서 앞 건물이 R와 B번 칠해진 값 중 작은 값에 현재 G색칠 비용 더한 값이 최소값입니다.
DP[i][2] : Math.min(DP[i+1][0], minDP[i+1][1]) + i번째 G색칠 비용
색깔 B을 사용하려면, 뒷 건물이 R, G로 칠해져야 진행해야합니다.
그래서 앞 건물이 R와 G번 칠해진 값 중 작은 값에 현재 B색칠 비용 더한 값이 최소값입니다.
예제입력에 설명을 보시면 진행되는 과정을 이해하기 편하실 것입니다.
※DP[0][0~2]를 구하지 않는 이유는 첫 번째 건물의 색을 고정하고 DP[][] 계산하기 때문입니다.
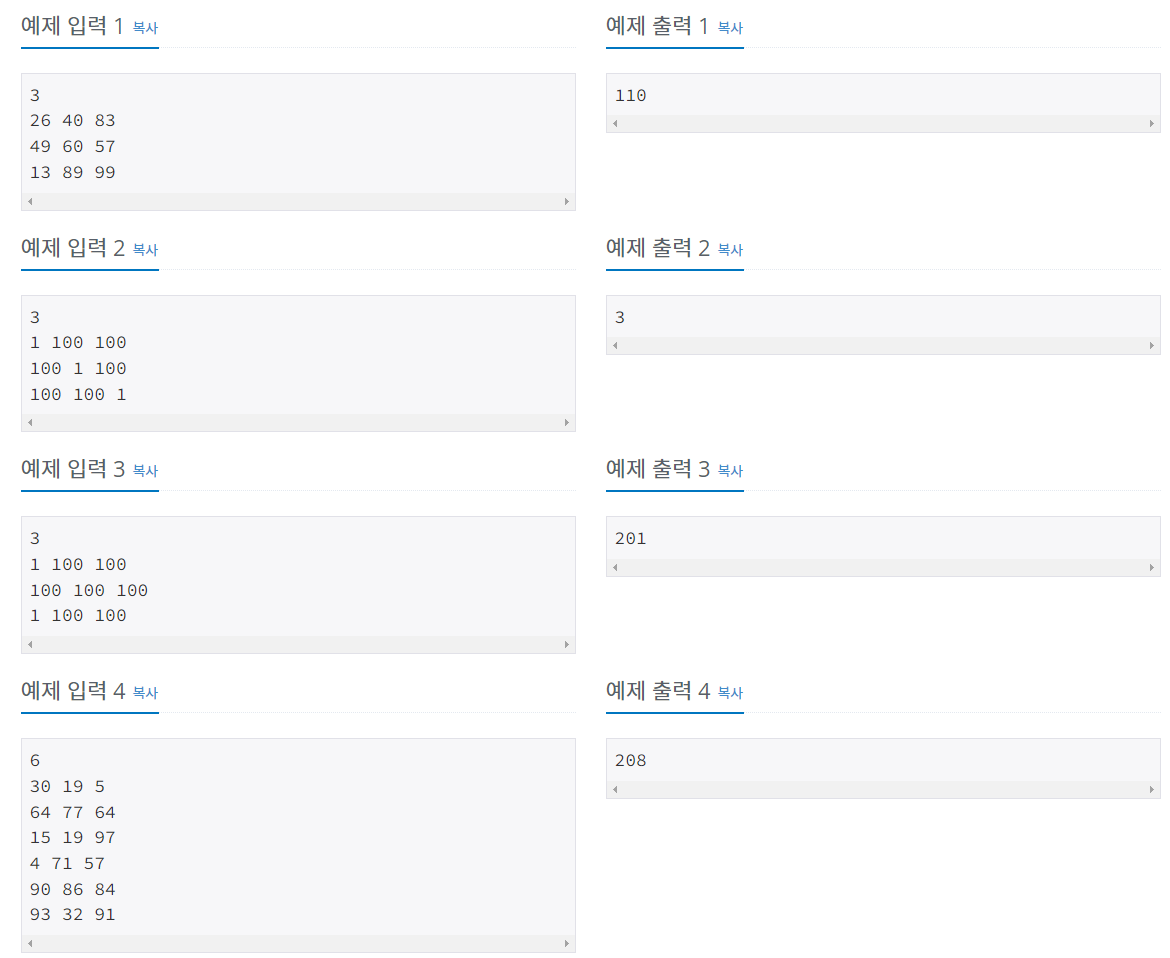
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 3
| 26 | 40 | 83 |
| 49 | 60 | 57 |
| 13 | 89 | 99 |
2. 첫 번째 건물의 색에 따른 마지막 건물부터 DP[][]를 구성하여 탐색합니다.
DP[] 탐색!
| 1 | 2 | |
| R | 138(49 + 89) | 1000001 |
| G | 159(60 + 99) | 89 |
| B | 146(57 + 89) | 99 |
첫 번째 건물이 R으로 색칠하였기 때문에 DP[1][0]은 접근 X, DP[1][1]와 DP[1][2] 중 작은 값을 선택합니다.
R : 146 + 26 = 172
| 1 | 2 | |
| R | 148(49 + 99) | 13 |
| G | 73(60 + 13) | 1000001 |
| B | 70(57 + 13) | 99 |
첫 번째 건물이 R으로 색칠하였기 때문에 DP[1][1]은 접근 X, DP[1][0]와 DP[1][2] 중 작은 값을 선택합니다.
G : 40 + 70 = 110
첫 번째 건물의 색이 B일 경우!
| 1 | 2 | |
| R | 138(49 + 89) | 13 |
| G | 73(60 + 13) | 89 |
| B | 70(57 + 13) | 1000001 |
첫 번째 건물이 R으로 색칠하였기 때문에 DP[1][2]은 접근 X, DP[1][0]와 DP[1][1] 중 작은 값을 선택합니다.
B : 83 + 70 = 153
3. 탐색이 끝나고 얻은 유지비의 최소값을 결과로 출력합니다.
R : 172
G : 110
B : 153
110 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 색을 칠하는 비용을 띄어쓰기 기준 나누었습니다.
- 첫 번째 건물의 색에 따른 DP[N-1][]값 초기화를 진행합니다.
- 점화식을 통해 DP[][]에 유지비의 최소값들을 저장합니다.
- 탐색으로 얻은 유지비의 최소값을 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
결과코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static int[][] DP, house; //DP : 메모이제이션, house : 색 칠하는 비용
static int N, firstColor;
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(br.readLine());
StringTokenizer st;
DP = new int[N][3];
house = new int[N][3];
//집 색칠하는 정보 저장
for(int i=0;i<N;i++) {
st = new StringTokenizer(br.readLine()," ");
house[i][0] = Integer.parseInt(st.nextToken());
house[i][1] = Integer.parseInt(st.nextToken());
house[i][2] = Integer.parseInt(st.nextToken());
}
int answer = Integer.MAX_VALUE;
//첫 번째 집을 RGB로 순서대로 칠했을 때
for(int i=0;i<3;i++) {
int result = Integer.MAX_VALUE;
//마지막 집 DP[][]값 초기화
for(int j=0;j<3;j++) {
if(j == i) {
DP[N-1][j] = 1000001; //마지막 집은 첫 번째 집과 동일한 색 X
continue;
}
DP[N-1][j] = house[N-1][j];
}
//DP[][] 점화식을 이용한 탐색
for(int j=N-2;j>0;j--) {
DP[j][0] = Math.min(DP[j+1][1], DP[j+1][2]) + house[j][0];
DP[j][1] = Math.min(DP[j+1][0], DP[j+1][2]) + house[j][1];
DP[j][2] = Math.min(DP[j+1][0], DP[j+1][1]) + house[j][2];
}
//현재 첫 번째 건물색 기준 최소 유지비 구하기
for(int j=0;j<3;j++) {
if(i == j)
continue;
result = Math.min(result, house[0][i] + DP[1][j]);
}
answer = Math.min(answer, result); //최소 유지비인지 비교!
}
bw.write(String.valueOf(answer)); //최소 유지비 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(수학,JAVA)2023번, 신기한 소수 (0) | 2023.02.10 |
|---|---|
| [백준] 알고리즘 분류(그래프 이론,JAVA)2252번, 줄 세우기 (0) | 2023.02.10 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)1647번, 도시 분할 계획 (0) | 2023.02.06 |
| [백준] 알고리즘 분류(그리디 알고리즘,JAVA)27313번, 효율적인 애니메이션 감상 (0) | 2023.02.05 |
| [백준] 알고리즘 분류(두 포인터,JAVA)2283번, 구간 자르기 (0) | 2023.02.03 |




댓글