문제 링크
9527번: 1의 개수 세기
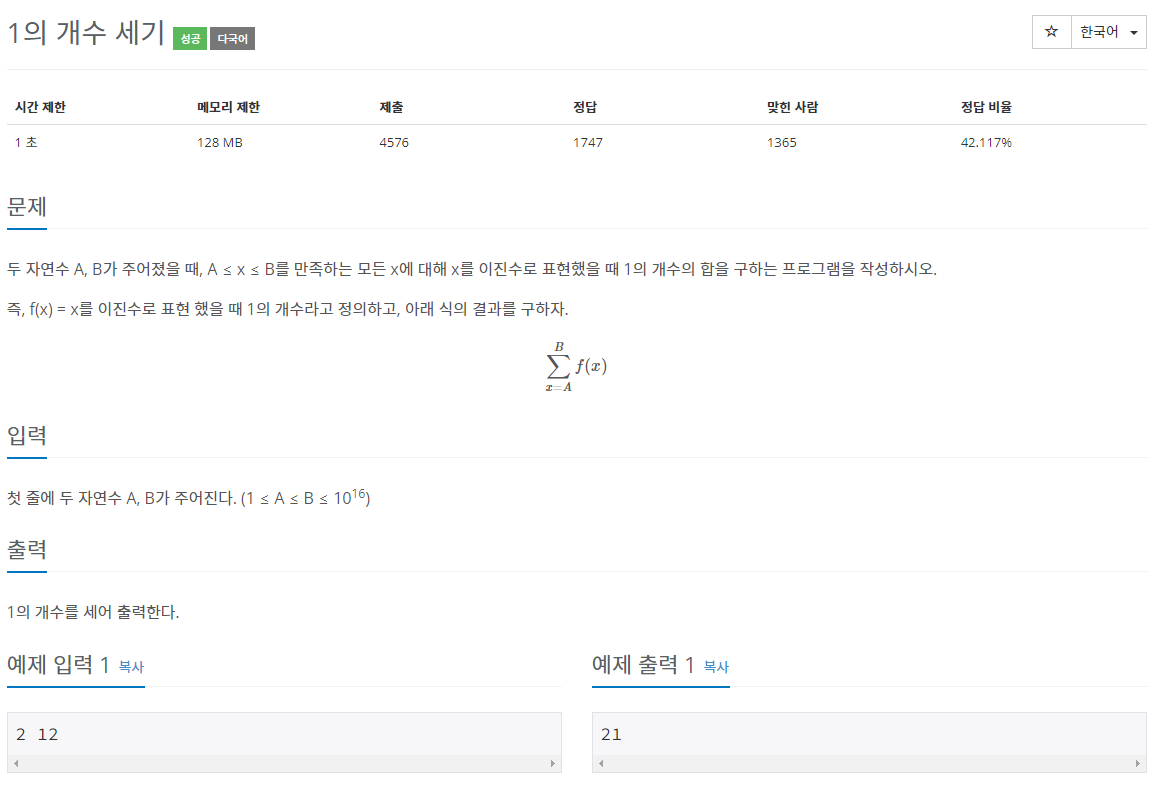
두 자연수 A, B가 주어졌을 때, A ≤ x ≤ B를 만족하는 모든 x에 대해 x를 이진수로 표현했을 때 1의 개수의 합을 구하는 프로그램을 작성하시오. 즉, f(x) = x를 이진수로 표현 했을 때 1의 개수라
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. A이상 B이하의 수들을 2진수로 표현할 때 1의 개수 결과로 출력합니다.
2. A와 B의 자연수 범위는 int형을 벗어나있습니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 2진수 1의 개수 누적합과 비트 마스킹을 이용하여 탐색합니다.
3. 탐색이 끝나고 얻은 1의 개수를 결과로 출력합니다.
2진수 1의 개수!
2진수의 1의 개수를 구할 때 규칙을 발견할 수 있습니다.
0 : 0
1 : 1
= 1개
= 누적합 : 1
10 : 1
11 : 2
= 3개 (1 + 2)
= 누적합 : 4
100 : 1
101 : 2
110 : 2
111 : 3
= 8개 (4 + 4 )
= 누적합 : 12
1000 : 1
1001 : 2
1010 : 2
1011 : 3
1100 : 2
1101 : 3
1110 : 3
1111 : 4
= 20개 (12 + 8)
= 누적합 : 32
점화식
DP[n] : 2ⁿ일 때 1의 개수 누적합

DP[0] = 1
DP[1] = 1 × 2 + 2¹ = 4
DP[2] = 4 × 2 + 2² = 12
DP[3] = 12 × 2 + 2³ = 32
...
DP[n] = DP[n-1] × 2 + 2ⁿ 이 성립하는 이유는
1000
1001
1010
1011
1100
1101
1110
1111
빨간색 부분은 DP[n-1]의 부분
파란색 부분은 1이 추가된 개수가 2ⁿ
누적합이므로 DP[n-1]
= DP[n-1] × 2 + 2ⁿ
누적합을 이용한 정수의 1의 개수 구하기
글로는 설명하기가 어려워서 예시로 보여드리겠습니다.
14에 대한 2진수 1의 개수 구할 때
14 = 1110
1110
빨간색 1이 나타나기까지 진행된 수는 000~111입니다.
000 ~ 111의 1의 개수는 DP[2] = 12개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
6[110]개, 1000일 때 1개가 추가적으로 존재할 것입니다.
12 + 6 + 1= 19개
1110
빨간색 1이 나타나기까지 진행된 수는 00~11입니다.
000 ~ 111의 1의 개수는 DP[1] = 4개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
2[10]개, 100일 때 1개가 추가적으로 존재할 것입니다.
4 + 2 + 1= 7개
1110
빨간색 1이 나타나기까지 진행된 수는 0~1입니다.
000 ~ 111의 1의 개수는 DP[0] = 1개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
0[0]개, 10일 때 1개가 추가적으로 존재할 것입니다.
1 + 0 + 1= 2개
19 + 7 + 2 = 28개
1~14(1110)까지의 1의 개수는 28개로 구할 수 있습니다.
예제입력 1.
1. 입력된 정보를 저장합니다.
A : 2
2. 2진수 1의 개수 누적합과 비트 마스킹을 이용하여 탐색합니다.
DP[] 누적합 구하기
DP[0] = 1
DP[1] = 1 × 2 + 2 = 4
DP[2] = 4 × 2 + 4 = 12
DP[3] = 12 × 2 + 8 = 32
....
12(1100)의 누적합
1100
빨간색 1이 나타나기까지 진행된 수는 000~111입니다.
000 ~ 111의 1의 개수는 DP[2] = 12개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
4[100]개, 1000일 때 1개가 추가적으로 존재할 것입니다.
12 + 4 + 1= 17개
1100
빨간색 1이 나타나기까지 진행된 수는 00~11입니다.
000 ~ 111의 1의 개수는 DP[1] = 4개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
0[00]개, 100일 때 1개가 추가적으로 존재할 것입니다.
4 + 0 + 1= 5개
1~12까지 1의 개수 : 17 + 5 = 22개
1(1)의 누적합
1
빨간색 1이 나타나기까지 진행된 수는 0입니다.
0의 1의 개수는 0개입니다.
이후 보라색 부분의 값들이 변할 때마다 빨간색 부분의 1은 항상 존재하기 때문에
0[0]개, 1일 때 1개가 추가적으로 존재할 것입니다.
1 ~ 1까지 1의 개수 : 0 + 0 + 1= 1개
12의 누적합 - 1의 누적합 : 22 - 1 = 21개
3. 탐색이 끝나고 얻은 1의 개수를 결과로 출력합니다.
21 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 A와 B를 저장합니다.
- setDp를 실행하여 DP[]의 배열에 2ⁿ 기준 1의 개수 누적합을 저장합니다.
- calOne을 이용하여 A ≤ n ≤ B의 포함된 1의 개수를 구합니다.
- 함수를 실행하여 얻은 1의 개수를 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- setDp함수는 점화식 DP[n] = DP[n-1] × 2 + 2ⁿ으로 1의 개수 누적합을 구합니다.
- calOne함수는 1 ~ N의 1의 개수를 DP[]를 이용하여 구합니다.
결과코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static long[] DP = new long[55]; //1의 개수 누적합 저장 배열
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//A(N)과 B(M)을 저장
long N = Long.parseLong(st.nextToken());
long M = Long.parseLong(st.nextToken());
setDp(); //누적합 계산!
//A ≤ n ≤ B : B의 누적합 - (A-1)의 누적합 구하기
long result = calOne(M) - calOne(N-1);
System.out.print(result); //A ≤ n ≤ B 의 1의 개수 출력
}
//1~N 정수에 대한 1의 개수 구하는 함수
static long calOne(long N) {
long count = N & 1;
//N보다 작은 2ⁿ의 n의 최대값
int size = (int) (Math.log(N)/Math.log(2));
//비트마스킹을 이용한 1의 개수 계산 진행
//DP[i-1] : 000 ~ 111 개수
//N - (1L << i) : 지정된 1이 반복 사용될 개수
// + 1 : 1000...
for(int i=size;i>0;i--) {
if((N & (1L<<i)) != 0L) {
count += DP[i-1] +(N - (1L<<i) + 1);
N -= (1L << i); //비트 이동시키기
}
}
return count; //1의 개수 반환
}
//DP[n] = DP[n-1] × 2 + 2ⁿ을 이용하여 누적합 저장하는 함수
static void setDp() {
DP[0] = 1; //DP[0]은 1으로 초기화
//점화식 적용
//DP[i-1] << 1 : DP[n-1] × 2
//1L << i : 2ⁿ
for(int i=1;i<55;i++)
DP[i] = (DP[i-1] << 1) + (1L << i);
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(다이나믹 프로그래밍,JAVA)1965번, 상자넣기 (0) | 2023.02.20 |
|---|---|
| [백준] 알고리즘 분류(그래프 이론,JAVA)9328번, 열쇠 (0) | 2023.02.19 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)1766번, 문제집 (0) | 2023.02.16 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)18126번, 너구리 구구 (0) | 2023.02.14 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)2623번, 음악프로그램 (0) | 2023.02.13 |




댓글