문제 링크
1637번: 날카로운 눈
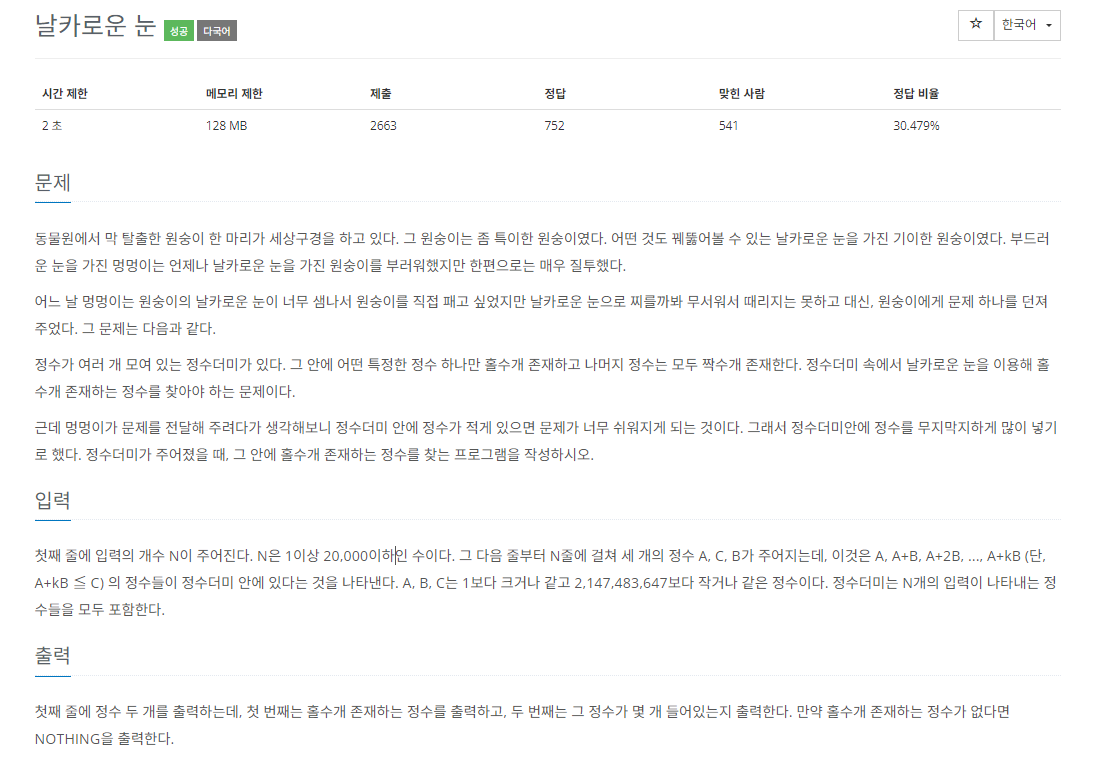
첫째 줄에 입력의 개수 N이 주어진다. N은 1이상 20,000이하인 수이다. 그 다음 줄부터 N줄에 걸쳐 세 개의 정수 A, C, B가 주어지는데, 이것은 A, A+B, A+2B, ..., A+kB (단, A+kB ≦ C) 의 정수들이 정수더미
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. N개의 정수 더미가 주어지며, A, B, C을 통해서 정수 더미의 속한 값을 구할 수 있습니다.
2. 정수 더미는 A, A + B, A + 2B ... ≤ C의 값들이 존재합니다.
3. 개수가 홀수인 정수는 항상 1개 혹은 존재하지 않습니다.(핵심!!)
4. 개수가 홀수인 정수와 개수를 결과로 출력합니다.
5. 홀수인 정수가 존재하지 않으면 "NOTHING"을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 이분탐색을 통해서 개수가 홀수인 정수를 탐색합니다.
3. 홀수인 정수가 존재하면 정수와 개수, 존재하지 않으면 NOTHING을 결과로 출력합니다.
정수의 개수
이 문제에서 " 개수가 홀수인 정수는 항상 1개 혹은 존재하지 않습니다." 이 부분이 핵심입니다.
Why??
개수가 홀수인 것이 1개만 존재한다면... 나머지는 짝수입니다.
짝수 + 짝수 = 짝수
짝수 + 홀수 = 홀수
홀수 + 홀수 = 짝수
위에 공식을 이용하면... 개수가 홀수인 정수가 존재한다면 항상 개수의 합을 진행해도 항상 홀수가 나와야 합니다.
개수의 합을 이용하기 위해서
fx(n) = n이하 정수가 존재하는 개수의 합이라고 표현해보겠습니다.
정수더미가
fx(1) = 2개
fx(5)에서 홀수가 나왔다는 의미 : 1 ~ 5까지의 정수 중에 홀수가 존재한다!!!!
각 정수 더미에 n이하의 정수가 몇 개 존재하는지 어떻게 구하느냐??
점화식을 통해서 구할 수 있습니다.
만약, n ≥ A일 때
(Math.min(C, 정수) - A) ÷ B + 1
(A : 1, B : 1, C : 5)
이 점화식이 성립하는 이유?
8에서 2의 배수의 개수를 구하려면
8 ÷ 2 = 4개로 구할 수 있습니다.
이 방식을 이용해서
정수 더미는 등차 수열의 형식이기 때문에 A에서 N의 배수만큼 증가하는 값들을 포함하고 있습니다.
A ≤ 정수 ≤ n 사이에 존재하는 B의 배수 개수 + 1(해당 정수)로 구할 수 있습니다.
위 방식을 이용해서 이분탐색을 진행하면 됩니다.
이분 탐색
max : 정수 더미에 C의 값중 가장 큰 값 + 1
fx(mid)가 홀수 일 때
right = mid
fx(mid) 가 짝수일 때
left = mid + 1;
... 위와 이분 탐색을 진행한 뒤
left == max : 홀수인 정수를 만나지 못했다
NOTHING을 결과로 출력합니다.
left != max : 홀수인 정수를 만났다
fx(left) - fx(left-1) : left의 정수의 개수
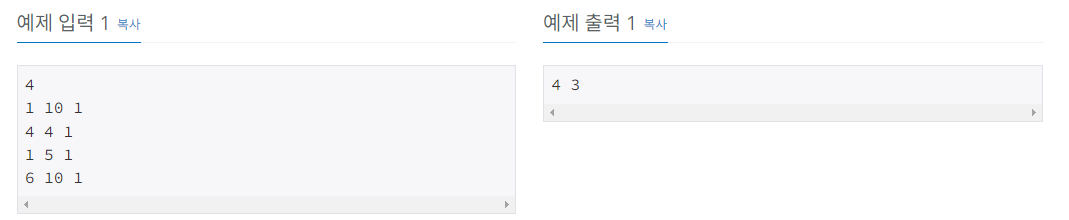
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 4
| A | C | B | |
| 정수더미 1 | 1 | 10 | 1 |
| 정수더미 2 | 4 | 4 | 1 |
| 정수더미 3 | 1 | 5 | 1 |
| 정수더미 4 | 6 | 10 | 1 |
2. 이분탐색을 통해서 개수가 홀수인 정수를 탐색합니다.
정수더미1 : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
max = 11
min = 1
left = 1
right = 11
mid = 6
fx(6) = 13개
홀수이므로, 6이하의 정수 중에서 홀수인 개수를 가진 정수가 존재합니다.
right = mid
left = 1
right = 6
mid = 3
fx(3) = 6개
짝수이므로, 3이하의 정수 중에서 홀수인 개수를 가진 정수가 존재하지 않습니다.
left = mid + 1
left = 4
right = 6
mid = 5
fx(5) = 11개
홀수이므로, 5이하의 정수 중에서 홀수인 개수를 가진 정수가 존재합니다.
right = mid
left = 4
right = 5
mid = 4
fx(4) = 9개
홀수이므로, 4이하의 정수 중에서 홀수인 개수를 가진 정수가 존재합니다.
right = mid
left와 right의 값이 같아져서, 홀수의 개수를 가지는 정수는 4입니다.
3. 홀수인 정수가 존재하면 정수와 개수, 존재하지 않으면 NOTHING을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 인형의 정보를 띄어쓰기 기준 구분합니다.
- fx함수를 이용해서 이분탐색을 진행합니다.
- 이분 탐색을 통해 홀수인 정수가 없으면 NOTHING을 BufferedWriter에 저장합니다.
- 이분 탐색을 통해 홀수인 정수가 있으면 fx(n) - fx(n-1)을 통해 정수의 개수를 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- fx함수는 fx(n)을 구현한 함수입니다.
- fx함수는 n이하의 정수가 정수 더미들에서 몇 개 존재하는지 구하는 함수입니다.
결과코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
StringTokenizer st;
int[][] arr = new int[N][3];
//C의 최대값
long min = Long.MAX_VALUE;
//A의 최소값
long max = Long.MIN_VALUE;
//입력값 저장
for(int i=0;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][2] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
//최대값, 최소값 계산
min = Math.min(min, arr[i][0]);
max = Math.max(max, arr[i][2]);
}
max++; //최대값 C + 1 진행
//이분 탐색을 위한 변수 설정
long left = min;
long right = max;
StringBuilder sb = new StringBuilder();
//이분 탐색 진행
while(left < right){
long mid = (left + right) / 2;
long temp = fx(arr, mid, N);
//fx(n)이 홀수일 때
if(temp % 2 == 1){
right = mid;
}else{ //fx(n)이 짝수일 때
left = mid + 1;
}
}
//홀수인 정수가 존재하지 않을 때
if(left == max){
sb.append("NOTHING");
}else{ //홀수인 정수가 존재할 때
//홀수인 정수의 개수 구하기 fx(n) - fx(n-1)
long result = fx(arr, left, N) - fx(arr, left-1, N);
sb.append(left).append(" ").append(result);
}
//결과 BufferedWriter 저장
bw.write(sb.toString());
bw.flush(); //결과 출력
bw.close();
br.close();
}
//fx(n) : n이하의 정수 개수 구하는 함수
static long fx(int[][] arr, long val, int N){
long cnt = 0;
for(int i=0;i<N;i++){
//점화식 조건을 만족하지 않을 때는 넘기기
if(arr[i][0] > val){
continue;
}
//점화식을 통한 개수 구하기
cnt += (Math.min(arr[i][2], val) - arr[i][0])/ arr[i][1] + 1;
}
return cnt; //정수 개수 반환
}
}
'백준' 카테고리의 다른 글
| [백준, Java] 13018번, 특이한 수열(애드 훅) (2) | 2023.10.09 |
|---|---|
| [백준, Java] 1637번, 작은 벌점(이분 탐색) (0) | 2023.10.05 |
| [백준, Java] 22988번, 재활용 캠페인(투 포인터, 정렬) (0) | 2023.09.14 |
| [백준, Java] 15565번, 귀여운 라이언(슬라이딩 윈도우) (0) | 2023.08.12 |
| [백준, Java] 16502번, 그녀를 찾아서(시뮬레이션) (0) | 2023.07.30 |




댓글