문제 링크
12944번: 재미있는 숫자 놀이
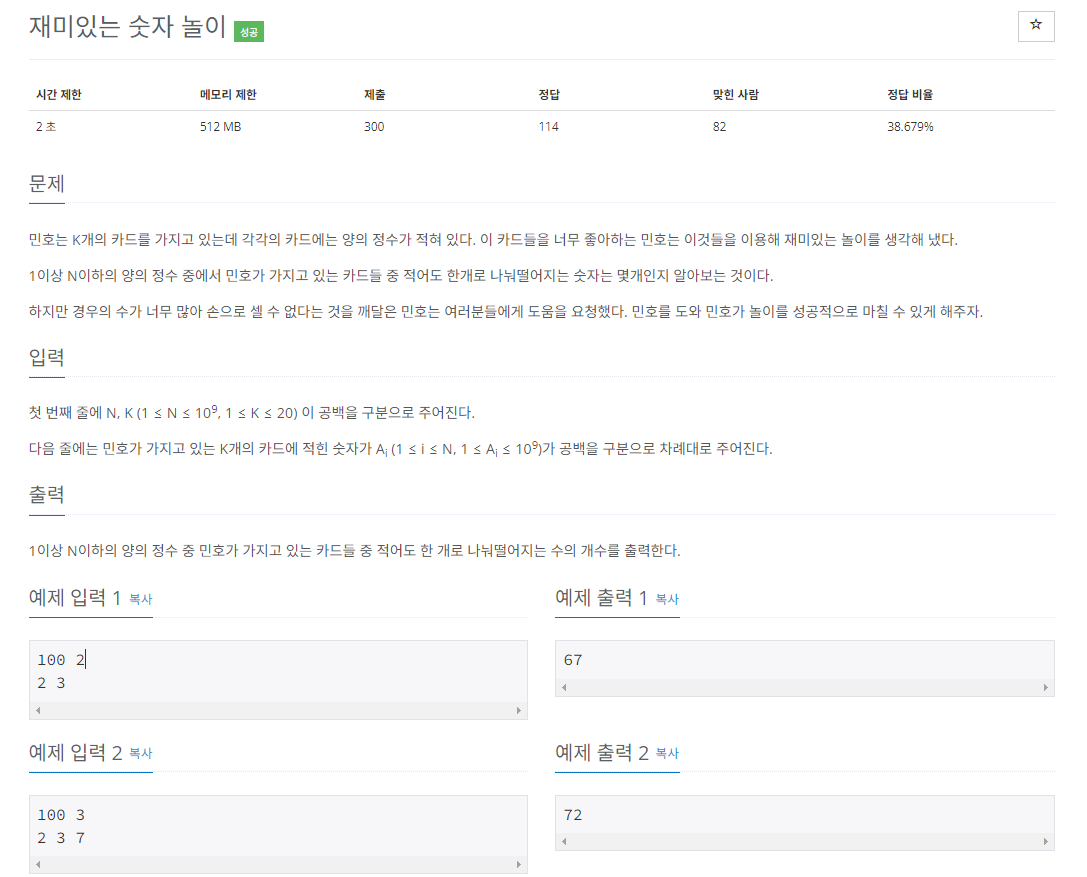
첫 번째 줄에 N, K (1 ≤ N ≤ 109, 1 ≤ K ≤ 20) 이 공백을 구분으로 주어진다. 다음 줄에는 민호가 가지고 있는 K개의 카드에 적힌 숫자가 Ai (1 ≤ i ≤ N, 1 ≤ Ai ≤ 109)가 공백을 구분으로 차례대로 주
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. 1부터 N이하의 양의 정수가 존재합니다.
2. 민호는 k개의 카드를 가지고 있습니다.
3. 양의 정수 중, 최소한 카드의 수로 나눠떨어지는 숫자의 개수를 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 나눠떨어지는 개수를 탐색합니다.
3. 나눠떨어지는 숫자의 개수를 결과로 출력합니다.
나눠떨어지는 수 탐색
정수론에서 100이하의 양수 중, 2로 나누어 떨어지는 개수
→ 즉, 2의 배수의 개수 : 100 ÷ 2 = 50개입니다.
위 방법을 이용하면, 각 카드가 1 ~ N까지 나눠떨어지는 개수를 알 수 있습니다.
하지만, 해당 값 중에서는 중복되는 값들이 존재할 것입니다.
중복되는 값을 찾는 것에서는 최소 공배수를 이용하여 구분하였습니다.
최소 공배수 점화식
lcm : a × b / gcd(a, b)
※ GCD : 최대 공약수
최대 공약수를 구하는 방법은 유클리드 호재법을 사용하였습니다. 자세한 정보는 아래 링크를 통해 개념을 학습하시는 것을 추천드립니다.
그러면, 최소 공배수만 구하면 되는 것이냐???
아닙니다!!, 최소 공배수 사이에도 중복되는 수들이 발생하기 때문입니다.
그러면... 어떻게 구분을 해야 하는가.... 포함배제의 원리를 사용해야 합니다.
포함배제의 원리 + 최소 공배수(LCM)을 통한 백트래킹 + 비트마스킹을 이용해서 탐색을 문제를 해결하였습니다.
포함배제의 원리를 이용하여 2가지 경우로 나눌 수 있습니다.
1. 홀수 개수의 최소 공배수일 때
→ 결과 += n / 최소 공배수
2. 짝수 개수의 최소 공배수일 때
→ 결과 -= n / 최소 공배수
예제입력 2.
1. 입력된 정보를 저장합니다.
N : 100
K : 3
| index | 1 | 2 | 3 |
| value | 2 | 3 | 7 |
2. 나눠떨어지는 개수를 탐색합니다.
비트마스킹 : 001
선택한 수 : { 2 }
개수 : 100 ÷ 2 = 50개
홀수 개의 최소 공배수이므로 덧셈을 합니다.
비트마스킹 : 010
선택한 수 : { 3 }
개수 : 100 ÷ 3 = 33개
홀수 개의 최소 공배수이므로 덧셈을 합니다.
비트마스킹 : 100
선택한 수 : { 7 }
개수 : 100 ÷ 7 = 14개
홀수 개의 최소 공배수이므로 덧셈을 합니다.
비트마스킹 : 011
선택한 수 : { 2, 3 }
최소 공배수 : 2 × 3 ÷ GCD(2, 3) = 2 × 3 ÷ 1 = 6
개수 : 100 ÷ 6 = 16개
짝수 개의 최소 공배수이므로 뺄셈을 합니다.
비트마스킹 : 101
선택한 수 : { 2, 7 }
최소 공배수 : 2 × 7 ÷ GCD(2, 7) = 2 × 7 ÷ 1 = 14
개수 : 100 ÷ 14 = 7개
짝수 개의 최소 공배수이므로 뺄셈을 합니다.
비트마스킹 : 110
선택한 수 : { 3, 7 }
최소 공배수 : 3 × 7 ÷ GCD(3, 7) = 3 × 7 ÷ 1 = 21
개수 : 100 ÷ 21 = 4개
짝수 개의 최소 공배수이므로 뺄셈을 합니다.
비트마스킹 : 111
선택한 수 : { 2, 3, 7 }
최소 공배수 : 2 × 3 × 7 ÷ GCD(2, 3, 7) = 2 × 3 × 7 ÷ 1 = 42
개수 : 100 ÷ 42 = 2개
홀수 개의 최소 공배수이므로 덧셈을 합니다.
3. 나눠떨어지는 숫자의 개수를 결과로 출력합니다.
얻은 개수들을 연산 진행
50 + 33 + 14 - 16 - 7 - 4 + 2 = 72
72을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 카드의 정보를 띄어쓰기 기준 나누었습니다.
- search함수를 실행하여 나눠떨어지는 수를 탐색합니다.
- 탐색이 끝난 뒤 나눠떨어지는 수의 개수를 결과로 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- search함수는 포함배제의 원리와 최소 공배수를 이용한 백트래킹으로 나눠떨어지는 수를 탐색합니다.
- lcm함수는 gcd함수를 이용하여 최소 공배수 점화식을 진행합니다.
- gcd함수는 유클리드 호재법을 이용하여 최대 공약수를 구합니다.
결과코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
//fullMask : 모든 수 방문 비트마스킹
//result : 결과값
static int fullMask, result, n, k;
//중복 연산을 배제하기 위한 메모이제이션
static boolean[] visited;
static long[] cards;
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw= new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//입력값 저장
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
//fullMask Setting
fullMask = (1 << k) - 1;
cards = new long[k];
visited = new boolean[fullMask+1];
st = new StringTokenizer(br.readLine()," ");
//카드 정보 저장
for(int i=0;i<k;i++){
cards[i] = Long.parseLong(st.nextToken());
}
//포함배제 원리 및 최소 공배수를 이용한 백트래킹 진행
for(int i=0;i<k;i++){
search(1, 1 << i, cards[i]);
}
//최소 한 번은 나눠떨어지는 수의 개수 BufferedWriter 저장
bw.write(String.valueOf(result));
bw.flush(); //결과 출력
bw.close();
br.close();
}
//백트래킹 및 메모이제이션을 통해서 나눠떨어지는 수 찾는 함수
static void search(int depth, int bitMask, long value){
//이미 연산한 경우
if(visited[bitMask]){
return;
}
//연산 확인
visited[bitMask] = true;
//홀수 개의 최소 공배수 일 때
if(depth % 2 == 1){
result += n / value;
}else{ //짝수 개의 최소 공부새우리 때
result -= n / value;
}
//모든 수를 사용하거나, 최소 공배수가 n보다 커질 때
if(bitMask == fullMask || value > n){
return;
}
//사용할 수 탐색
for(int i=0;i< k;i++){
//이미 사용했던 수면 넘기기
if((bitMask & (1 << i)) != 0){
continue;
}
//재귀 진행
search(depth+1, bitMask | (1 << i), lcm(value, cards[i]));
}
}
//점화식을 이용한 최소 공배수 구하는 함수
static long lcm(long value, long card){
if(value > card){
return value * card / gcd(value, card);
}else{
return value * card / gcd(card, value);
}
}
//유클리드 호재법을 이용한 최대 공약수 구하는 함수
static long gcd(long a, long b){
if(b == 0){
return a;
}
return gcd(b, a % b);
}
}
'백준' 카테고리의 다른 글
| [백준, Java] 1441번, 나누어 질까(정수론) (2) | 2023.10.29 |
|---|---|
| [백준, Java] 3142번, 즐거운 삶을 위한 노력(정수론) (2) | 2023.10.26 |
| [백준, Java] 14252번, 공약수열(정수론) (4) | 2023.10.22 |
| [백준, Java] 12979번, 종이 접기(정수론) (0) | 2023.10.18 |
| [백준, Java] 19942번, 다이어트(백트래킹) (0) | 2023.10.13 |




댓글