문제 링크
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
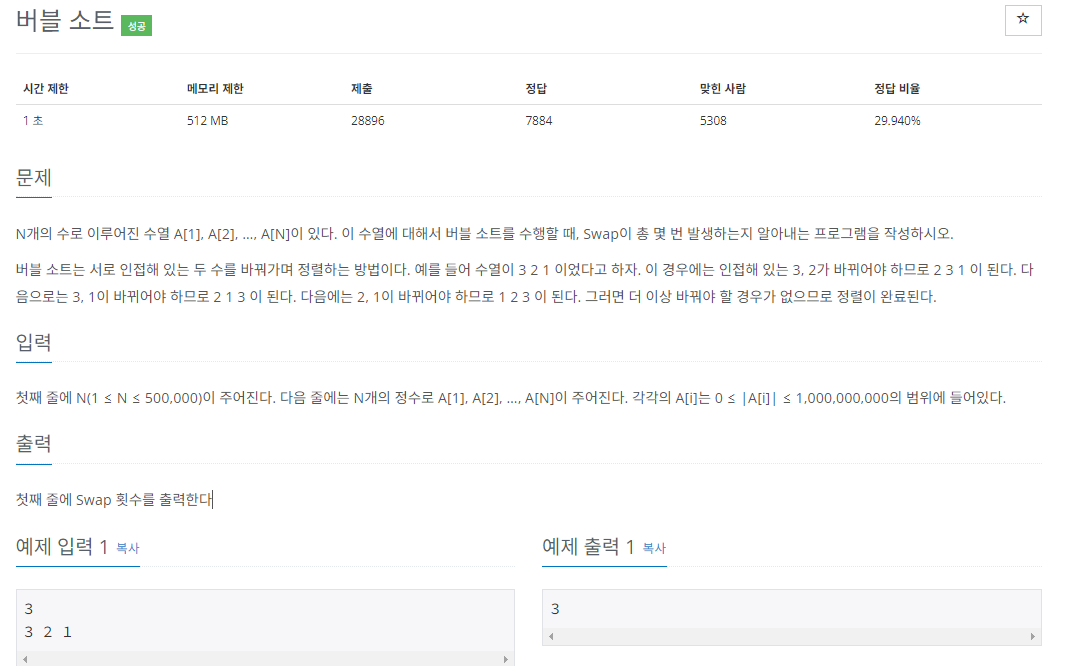
접근 방법
이 문제에 핵심
1. 수열 A에 대해서 버블 정렬을 진행했을 때 Swap이 발생하는 횟수를 결과로 출력합니다.
2. A[i]의 값은 Integer 범위 안에 존재합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 세그먼트 트리로 각 수열의 작은 값부터 저장함으로써 Swap의 개수를 탐색합니다.
3. 탐색한 Swap의 개수를 결과로 출력합니다.
버블 정렬이란??
※ 버블 정렬에 기초적 개념은 아래 링크에서 학습하시는 것을 추천드립니다.
버블 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 버블 정렬 또는 거품 정렬(-整列, 영어: bubble sort 버블 소트[*], sinking sort 싱킹 소트[*])은 정렬 알고리즘 중 하나이다. 시간 복잡도가 O ( n 2 ) {\displaystyle O(n^{2})}
ko.wikipedia.org
아래와 같은 수열에서 버블 정렬을 진행하면
| 5 | 4 | 3 | 2 | 1 |
| 4 | 5 | 3 | 2 | 1 |
| 4 | 3 | 5 | 2 | 1 |
...
| 1 | 2 | 3 | 4 | 5 |
Swap한 횟수(큰 값 기준)
※큰 값 기준은 Swap을 진행했을 때 큰 값을 기준으로 Swap을 진행했다고 표현하는 것입니다.
| 5 | 4 | 3 | 2 | 1 |
| 4번 | 3번 | 2번 | 1번 | 0번 |
점화식
i번째 값의 Swap 개수 : i이후의 값들 중 작은 값의 개수
5 : { 4, 3, 2, 1 }, 4개
4 : { 3, 2, 1 }, 3개
3 : { 2, 1 }, 2개
2 : { 1 }, 1개
1 : {}, 0개
세그먼트 트리(수열의 값 저장 및 Swap 개수 구하기)
※ 세그먼트 트리에 기초적 개념은 아래 링크에서 학습하시는 것을 추천드립니다.
Swap의 개수가 "작은 수의 개수"에 결정나기 때문에 수열의 작은 수부터 세그먼트 트리에 저장을 시작합니다.→ 작은 값들부터 저장했기 때문에 현재 저장되는 값은 지금 세그먼트 트리의 저장된 값들보다 항상 크다는 것을 증명할 수 있습니다.
세그먼트 트리를 통해서 탐색할 때 순서는
1. 현재 세그먼트 트리에서 Swap개수 구하기
2. 현재 값 세그먼트 트리에 저장하기!
※ 같은 값이 여러개 있는 경우 한 번에 모아서 해야 합니다!!
예를 들어, 아래와 같은 수열 A에 대해서 버블 정렬을 진행할 때 세그먼트 트리의 변화
| index | 0 | 1 | 2 | 3 | 4 |
| num | 5 | 3 | 1 | 2 | 1 |
초기 세그먼트 트리
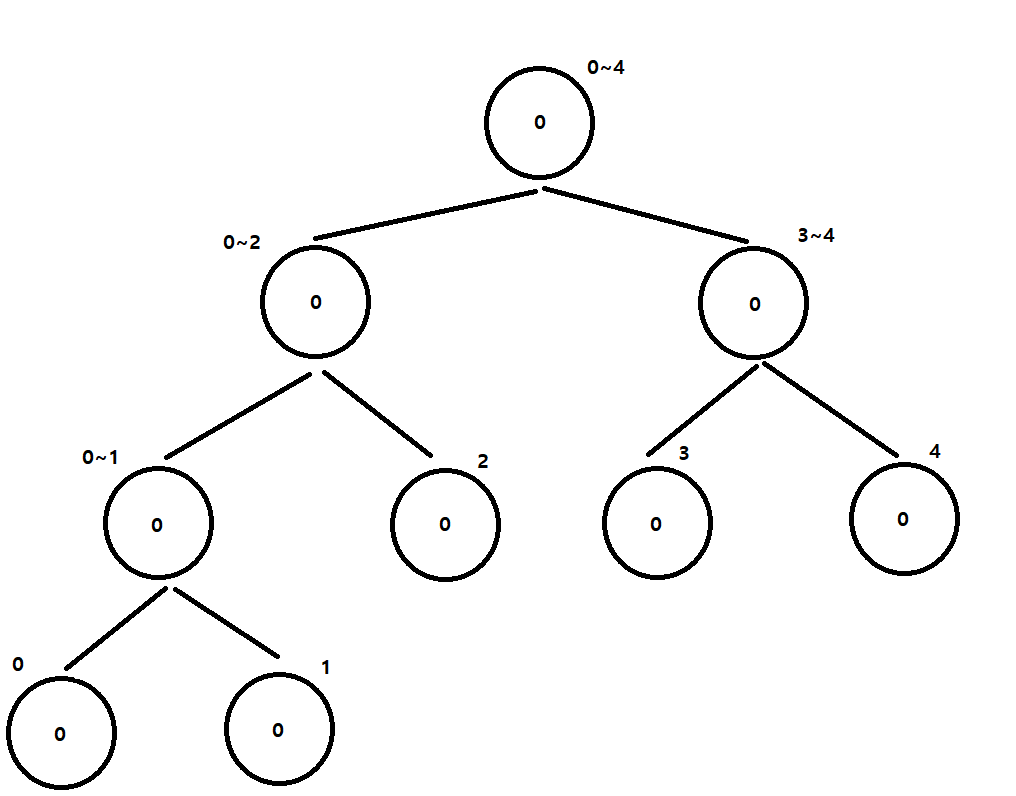
작은 값부터 탐색 진행!
| index | 0 | 1 | 2 | 3 | 4 |
| num | 5 | 3 | 1 | 2 | 1 |
현재 세그먼트 트리에서 Swap 횟수 계산
index(2)인 1 : [3 ~ 4] 범위에 작은 값 개수 찾아보기
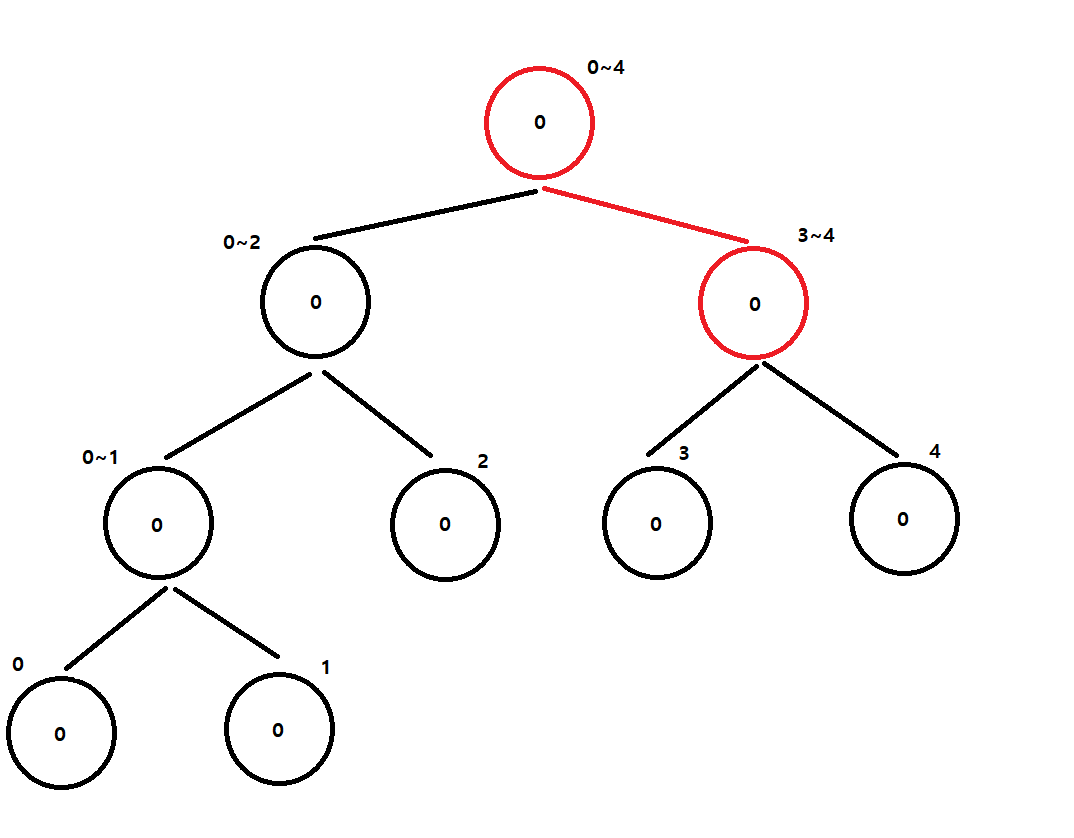
Swap 횟수 : 0번[3 ~ 4]
index(4)인 1 : 더 큰 값이 존재하지 않기 때문에 Swap 횟수는 0번
세그먼트 트리에 저장하기!
index(4)인 1, index(2)인 1,
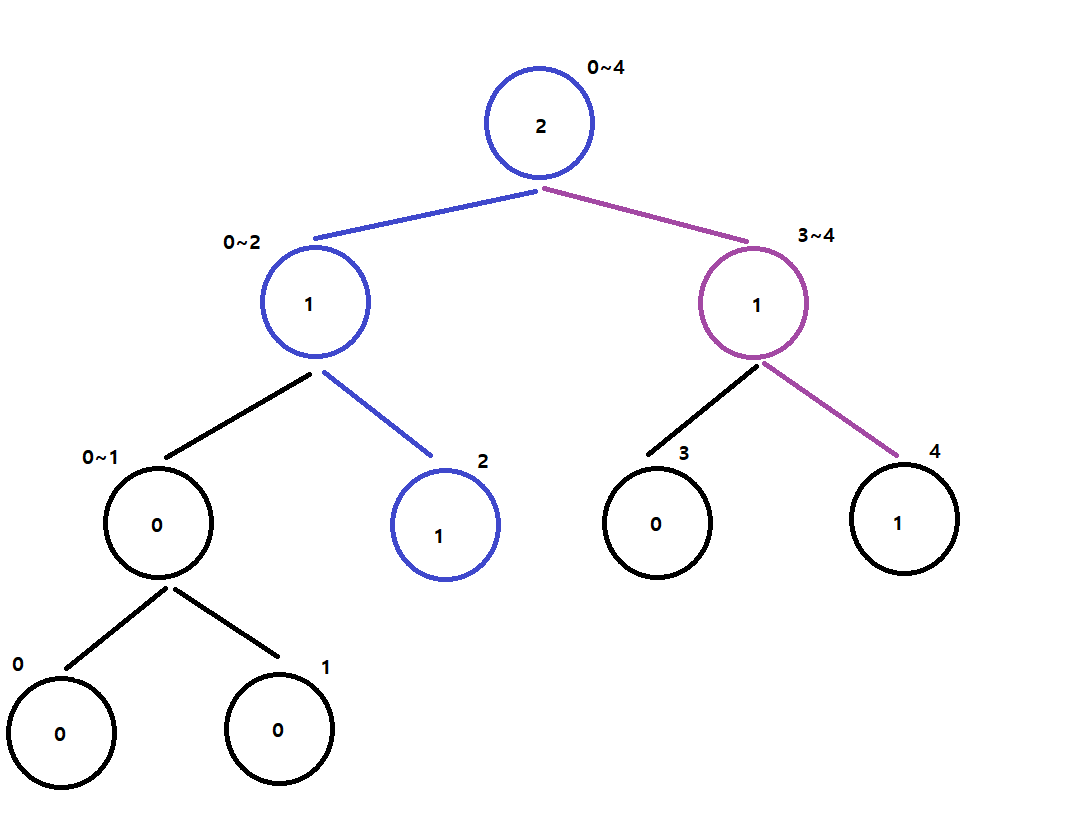
다음 작은 값부터 탐색 진행!
| index | 0 | 1 | 2 | 3 | 4 |
| num | 5 | 3 | 1 | 2 | 1 |
현재 세그먼트 트리에서 Swap 횟수 계산
index(3)인 2 : [4] 범위에 작은 값 개수 찾아보기
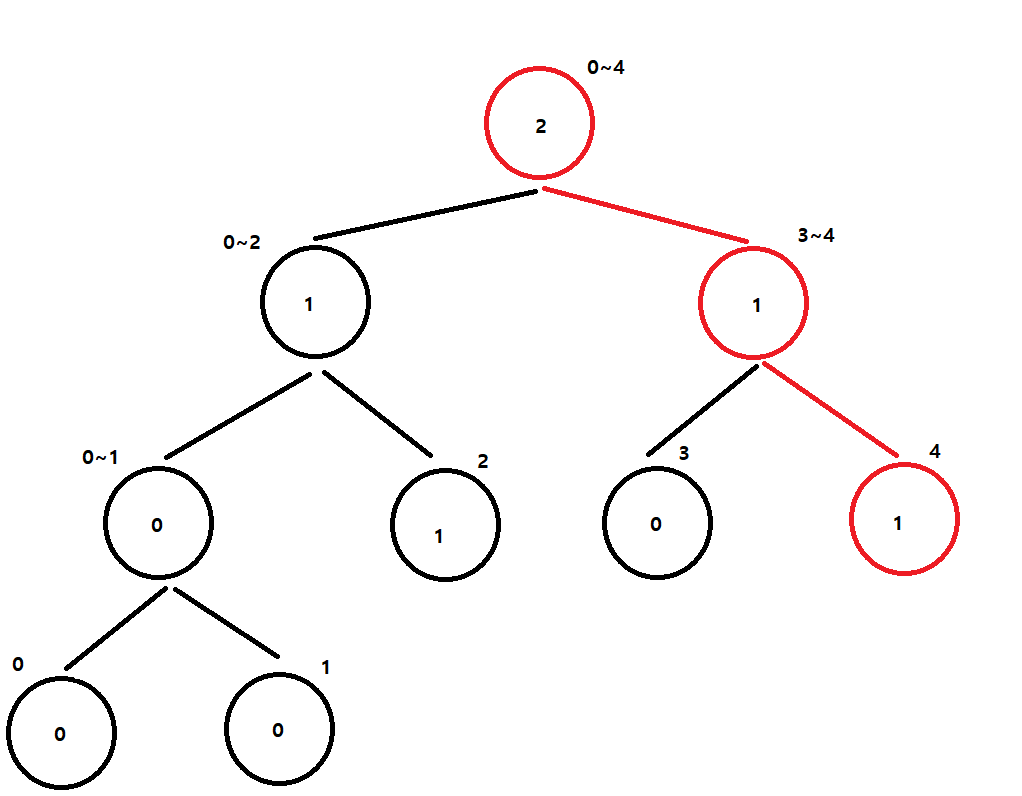
Swap 횟수 : 1번[4]
세그먼트 트리에 저장하기!
index(3)인 2
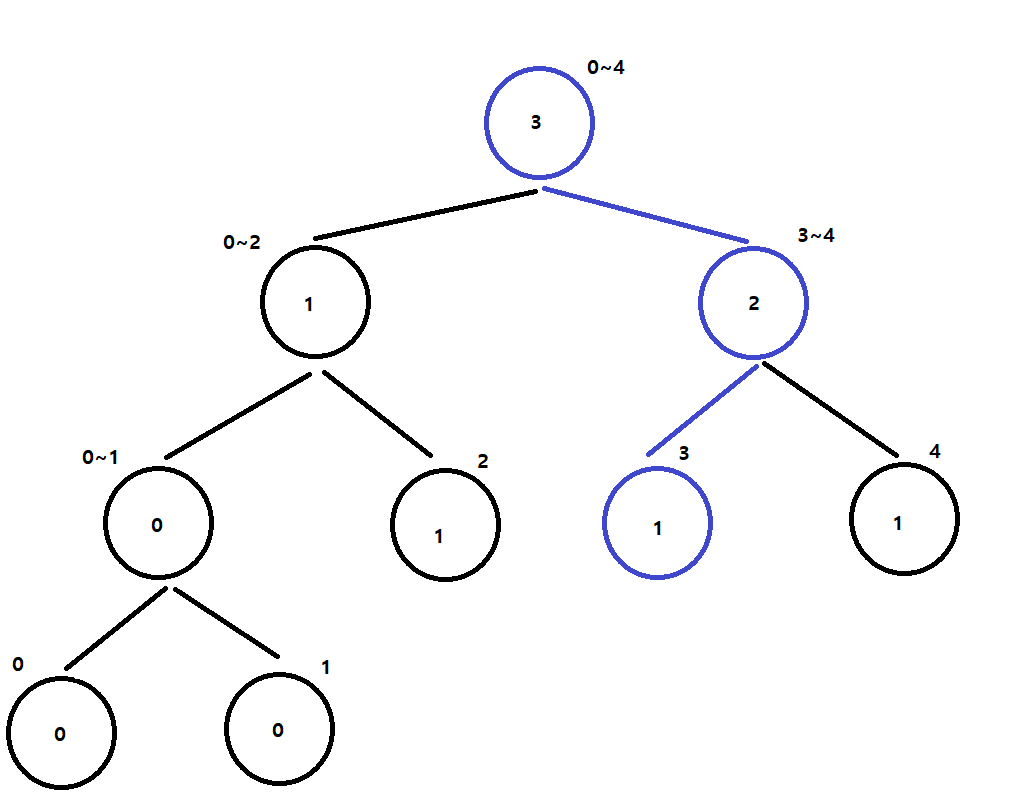
다음 작은 값부터 탐색 진행!
| index | 0 | 1 | 2 | 3 | 4 |
| num | 5 | 3 | 1 | 2 | 1 |
현재 세그먼트 트리에서 Swap 횟수 계산
index(1)인 3 : [2~4] 범위에 작은 값 개수 찾아보기
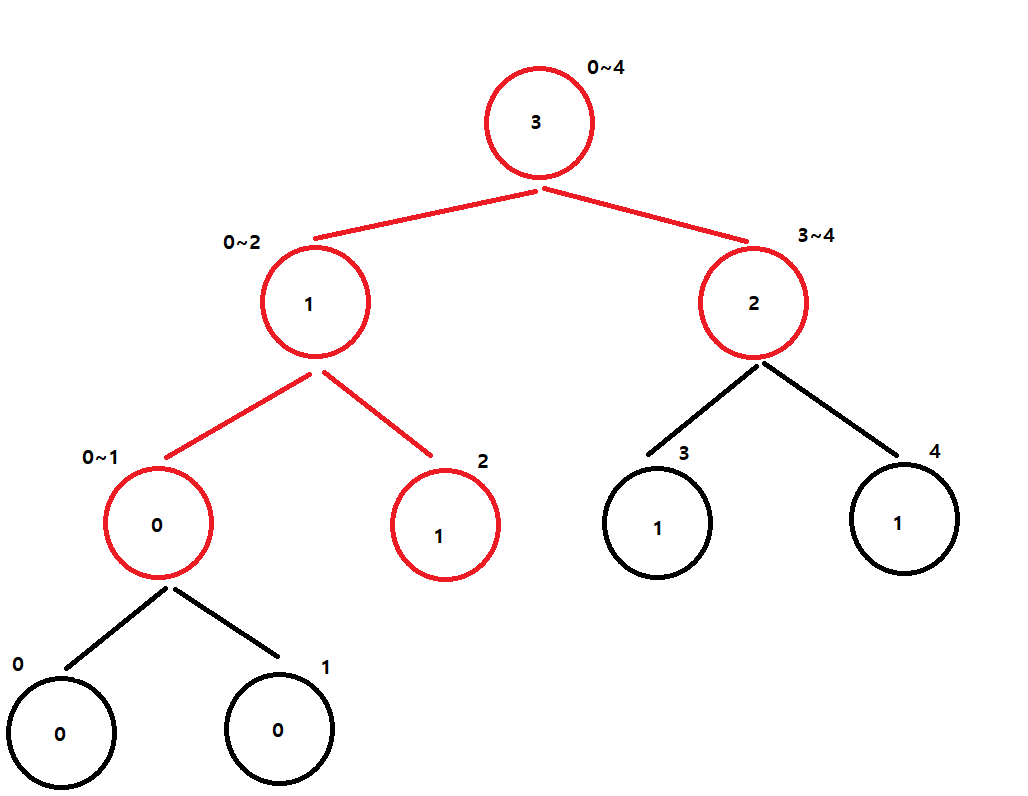
Swap 횟수 : 1번[2] + 2번[3~4] = 3번
세그먼트 트리에 저장하기!
index(1)인 3

다음 작은 값부터 탐색 진행!
| index | 0 | 1 | 2 | 3 | 4 |
| num | 5 | 3 | 1 | 2 | 1 |
현재 세그먼트 트리에서 Swap 횟수 계산
index(0)인 5 : [1~4] 범위에 작은 값 개수 찾아보기

Swap 횟수 : 1번[1] + 1번[2] + 2번[3~4] = 4번
세그먼트 트리에 저장하기!
index(0)인 5
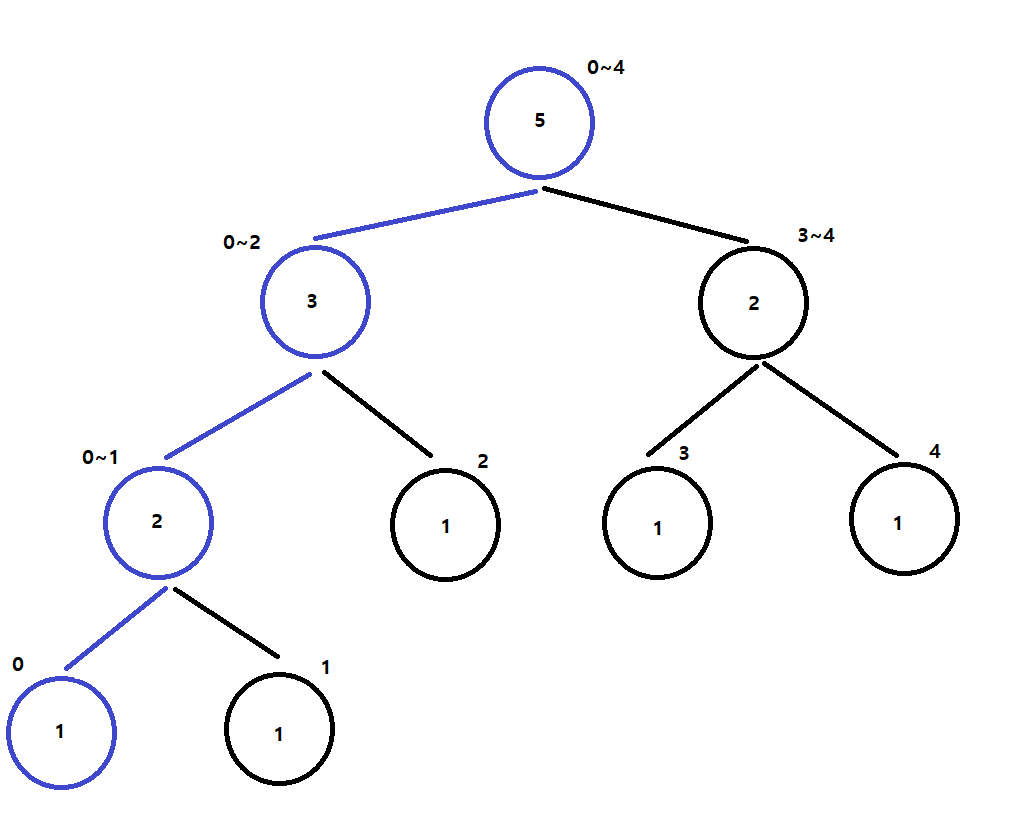
총 Swap 개수 : 0 + 0 + 1 + 3 + 4
※예제 입력 진행 과정은 위 수열보다 내용이 간단하기 때문에 생략하도록 하겠습니다.
예제입력 1.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 수열의 정보를 띄어쓰기 기준 저장합니다.
- 수열을 오름차순 정렬으로 정렬합니다.
- 수열의 작은 수부터 search, update함수를 통해서 Swap개수와 세그먼트 트리를 최신화합니다.
- 탐색을 통해 얻은 Swap 횟수를 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- search함수는 세그먼트 트리에서 범위에 합을 구합니다.
- update함수는 세그먼트 트리에서 최신화 및 수의 저장을 진행합니다.
- getTreeSize은 세그먼트 트리에 최대 크기를 구합니다.
결과코드
import java.io.*;
import java.util.*;
public class Main {
//수열의 index와 숫자를 저장하는 클래스
static class Info implements Comparable<Info> {
int idx, val;
Info(int idx, int val){
this.idx = idx;
this.val = val;
}
//숫자 기준 오름차순 정렬
@Override
public int compareTo(Info o) {
return this.val - o.val;
}
}
//세그먼트 트리 구현할 배열
static long[] tree;
//수열 A의 저장 배열
static Info[] values;
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine()," ");
values = new Info[N];
//수열 A에대한 입력값 저장
for(int i=0;i<N;i++){
values[i] = new Info(i, Integer.parseInt(st.nextToken()));
}
long result = 0;
//오름차순 정렬
Arrays.sort(values);
//세그먼트 트리 관련 배열 초기화
tree = new long[getTreeSize(N)];
int pre = Integer.MAX_VALUE;
List<Integer> idxs = new ArrayList<>();
//Swap 개수 구하기 시작!(작은 값부터 탐색)
for(Info val : values){
//같은 값이 아닌 더 큰 값이 들어왔을 때
if(pre != val.val){
//이전 같은 값들 세그먼트 트리에 저장
for(int idx : idxs){
update(0, N-1, 1, idx);
}
//같은 값들 초기화
idxs.clear();
pre = val.val;
}
//현재 세그먼트 트리에서 Swap 개수 구하기
result += search(0, N-1, 1, val.idx+1, N-1);
//같은 값 Index정보 저장
idxs.add(val.idx);
}
//Swap 개수 BufferedWriter 저장
bw.write(String.valueOf(result));
bw.flush(); //결과 출력
bw.close();
br.close();
}
//세그먼트 트리에서 Swap개수 구하는 함수(범위에 합)
static long search(int start, int end, int node, int left, int right){
//구하는 범위를 벗어났을 때
if(left > end || right < start) {
return 0L;
}
//구하는 범위에 속했을 때
if(left <= start && end <= right){
return tree[node];
}
//하위 노드 탐색
int mid = (start + end) / 2;
return search(start, mid, node*2, left, right) + search(mid+1, end, node*2 + 1, left, right);
}
//세그먼트 트리에 현재 값 저장 및 최신화
static void update(int start, int end, int node, int idx){
//리프 노드일 때
if(idx == start && idx == end){
tree[node] = 1L;
return;
}
//하위 노드 탐색
int mid = (start + end) / 2;
if(idx <= mid){
update(start, mid, node * 2, idx);
}else{
update(mid + 1, end, node * 2 + 1, idx);
}
//세그먼트 트리 노드 값 최신화
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
//세그먼트 트리의 노드 개수 구하는 함수
static int getTreeSize(int n) {
int h = (int)Math.ceil(Math.log(n)/Math.log(2))+1;
return (int)Math.pow(2, h)-1;
}
}
'백준' 카테고리의 다른 글
| [백준, Java] 15573번, 채굴(이분 탐색, BFS) (4) | 2023.12.22 |
|---|---|
| [백준, Java] 2866번, 문자열 잘라내기(이분 탐색) (2) | 2023.12.12 |
| [백준, Java] 12991번, 홍준이의 행렬(이분탐색) (0) | 2023.12.09 |
| [백준, Java] 1497번, 기타콘서트(백트래킹) (0) | 2023.12.09 |
| [백준, Java] 1981번, 배열에서 이동(BFS, 이분탐색) (2) | 2023.12.04 |




댓글