문제 링크
17611번: 직각다각형
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명


접근 방법
이 문제에 핵심
1. N개의 꼭지점을 지나는 단순직각다각형이 존재합니다.
2. 수평/수직 선분은 다각형의 어떤 선분에도 겹치지 않아야 합니다.
3. 임의의 수직/수평 선분 중 가장 많이 교차하는 점의 개수를 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 단순직각다각형을 그리면서 누적합을 통해 가장 많이 교차하는 점의 개수룰 탐색합니다.
3. 탐색을 통해 최대 교차하는 점의 개수를 결과로 출력합니다.
누적합(교차하는 점의 개수)

(0, 0) → (0, 1)을 갈 때 y축의 0 < y < 1 사이의 수평직선은 항상 지나게 됩니다.
즉, 선분을 이동할 때마다 수직/수평의 n < x/y < n + 1 의 선분을 교차하게 된다는 것입니다.
이를 통해서 배열에서 Index가 가리키는 값은 i < y < i + 1 범위를 뜻하게 됩니다.
1 : 1 ~ 2를 기준으로 수직/수평 선분과 교차하는 점의 개수
3 : 3 ~ 4를 기준으로 수직/수평 선분과 교차하는 점의 개수
...
이후, 입력되는 점의 개수를 받을 때마다, 수직/수평에 대한 교차하는 점의 개수를 누적합을 통해서 쌓아가면 됩니다.

위 그림에서는 index : {0, 1, 2, 3}을 가리키는 수직 선분에 교차점 개수의 +1씩 누적합을 진행합니다.
이후, 모든 수직/수평 선분의 교차점의 개수 중 가장 큰 값을 결과로 출력하면 됩니다.
★마지막 꼭지점은 출발 꼭지점으로 돌아가야 단순직각다각형을 만들 수 있으므로 이 부분을 생각하셔야 합니다.
※예제 입력 과정을 살펴보시면 이해하시기 편하실 것입니다.
예제입력 2.
1. 입력된 정보를 저장합니다.
N : 12

2. 단순직각다각형을 그리면서 누적합을 통해 가장 많이 교차하는 점의 개수룰 탐색합니다.
꼭지점들을 순차적으로 그으며 누적합을 진행하면 아래 그림과 같이 진행됩니다.
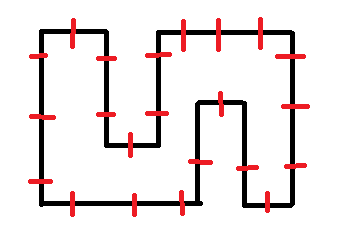
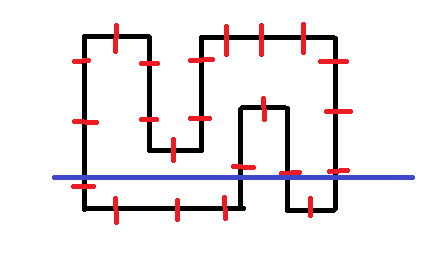


3. 탐색을 통해 최대 교차하는 점의 개수를 결과로 출력합니다.
6을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 꼭지점의 정보를 띄어쓰기 기준 나누었습니다.
- 꼭지점을 순서대로 그으며 단순직각다각형을 만듭니다.
- 단순직각다각형을 만들면서 xLineSearch와 yLineSearch를 통해 누적합을 진행합니다.
- 단순직각다각형이 완성되었을 때 누적합으로 구한 최대 교차점의 개수를 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- xLineSearch는 두 꼭지점을 이을 때 수평선분일 때 누적합을 진행합니다.
- yLineSearch는 두 꼭지점을 이을 때 수직선분일 때 누적합을 진행합니다.
결과코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//첫 꼭지점 정보 저장
int[][] sum = new int[1000001][2];
int x = Integer.parseInt(st.nextToken()) + 500000;
int y = Integer.parseInt(st.nextToken()) + 500000;
//시작 꼭지점 변수로 저장
int startX = x;
int startY = y;
//단순직각다각형 만들면서 누적합 진행
for(int i=1;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
int curX = Integer.parseInt(st.nextToken()) + 500000;
int curY = Integer.parseInt(st.nextToken()) + 500000;
//수직 선분일 때
if(x == curX){
yLineSearch(sum, y, curY);
}else{ //수평 선분일 때
xLineSearch(sum, x, curX);
}
//이전 꼭지점 변경
x = curX;
y = curY;
}
//마지막 꼭지점과 첫 번째 곡지점 연결
if(x == startX) {
yLineSearch(sum, y, startY);
}else{
xLineSearch(sum, x, startX);
}
int result = 0;
//최대값 탐색
for(int i=0;i<1000001;i++){
result = Math.max(result, Math.max(sum[i][0], sum[i][1]));
}
//최대 교차점의 개수 BufferedWriter 저장
bw.write(String.valueOf(result));
bw.flush(); //결과 출력
bw.close();
br.close();
}
//수직 선분일 때 누적합 진행하는 함수
static void xLineSearch(int[][] sum, int x, int curX){
if(x > curX) { //↓
for (int j = curX; j < x; j++) {
sum[j][0]++;
}
}else{ // ↑
for (int j = x; j < curX; j++) {
sum[j][0]++;
}
}
}
//수평 선분일 때 누적합 진행하는 함수
static void yLineSearch(int[][] sum, int y, int curY){
if(y > curY){ //←
for(int j=curY;j<y;j++){
sum[j][1]++;
}
}else{ //→
for(int j=y;j<curY;j++){
sum[j][1]++;
}
}
}
}'백준' 카테고리의 다른 글
| [백준, Java] 12101번, 1, 2, 3 더하기 2, (백트레킹) (2) | 2024.01.21 |
|---|---|
| [백준, Java] 14728번, 벼락치기(DP) (2) | 2024.01.11 |
| [백준, Java] 27210번, 신을 모시는 사당(누적합, DP) (4) | 2024.01.03 |
| [백준, Java] 17129번, 윌리암슨수액빨이딱따구리가 정보섬에 올라온 이유(BFS) (2) | 2023.12.27 |
| [백준, Java] 15573번, 채굴(이분 탐색, BFS) (4) | 2023.12.22 |




댓글