문제 링크
1438번: 가장 작은 직사각형
예제 1의 경우 (9,4), (9,6), (14,4), (14,6)을 꼭짓점으로 하는 직사각형을 만들면 된다.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
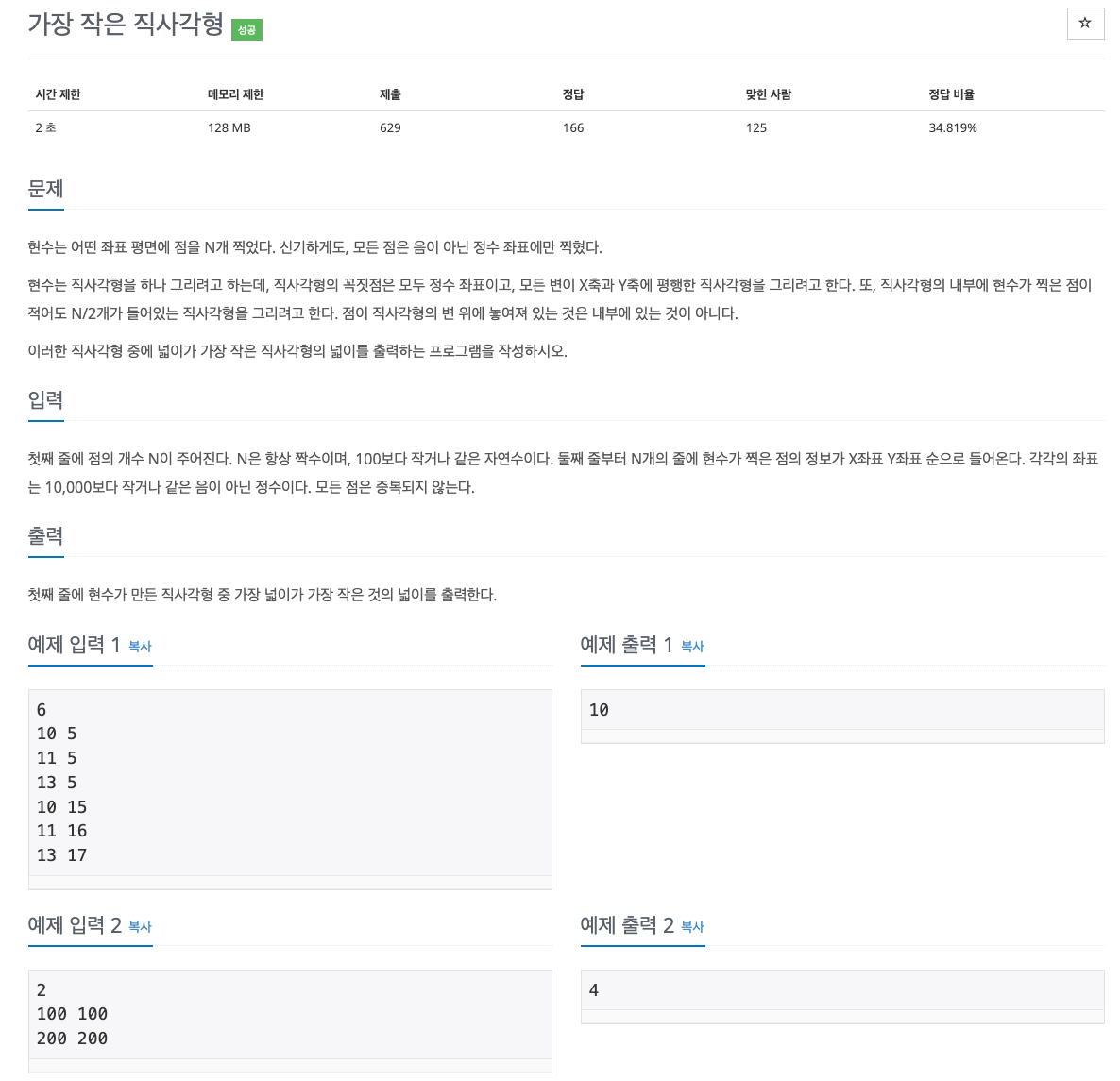
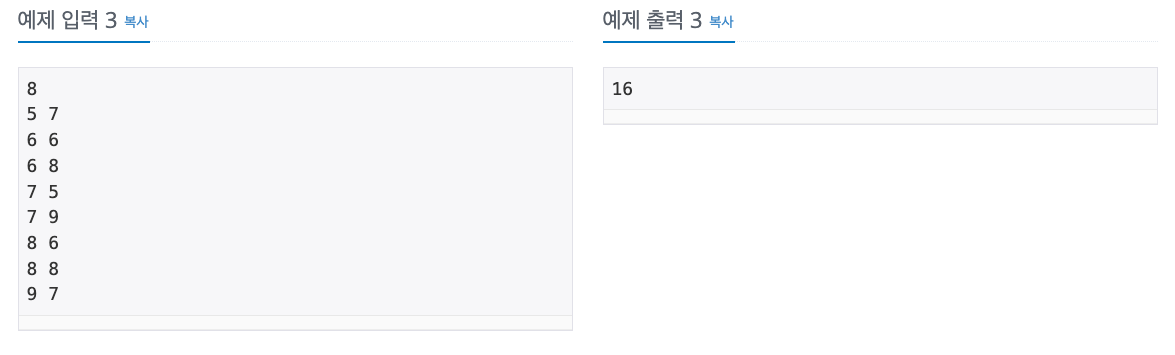
접근 방법
이 문제에 핵심
1. 좌표 평면에 점 N개를 찍었으며, 모든 점은 음수가 아닌 정수 좌표에 있습니다.
2. 직사각형을 그리는데 X/Y축과 평행한 직사각형이며, 찍은 점이 N/2개가 들어있는 직사각형을 그리려고 합니다.
3. 직사각형 변 위에 있는 점은 내부에 있는 것이 아닙니다.
4. 직사각형 중 가장 작은 직사각형의 넓이를 결과로 출력합니다.
5. N은 항상 짝수이며, 모든 점은 중복되지 않습니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 좌표의 상한/하한을 기준으로 조건에 만족하는 모든 직사각형을 탐색합니다.
3. 탐색을 통해 얻은 최소 직사각형의 넓이를 결과로 출력합니다.
좌표의 상한과 하한
모든 좌표를 기준으로 직사각형을 그리면 좌표의 최대값이 ( 0, 0 ) ~ ( 10000, 10000 )으로써 시간초과가 발생합니다.
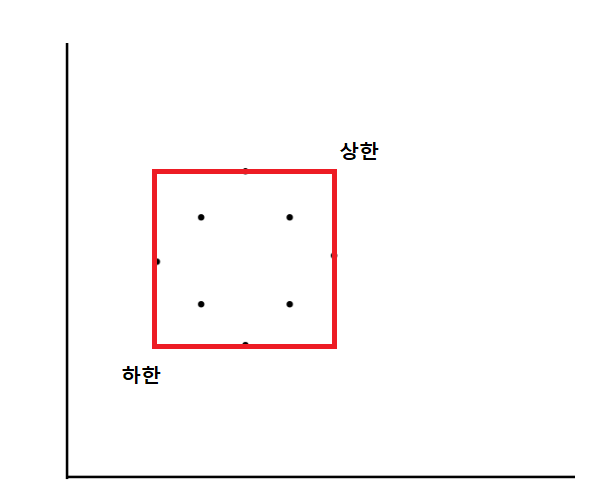
좌표가 주어지면 최소 좌표와 최대의 좌표를 구할 수 있습니다. 그림으로 살펴보면

위 그림처럼 직사각형의 하한과 상한을 구할 수 있습니다.
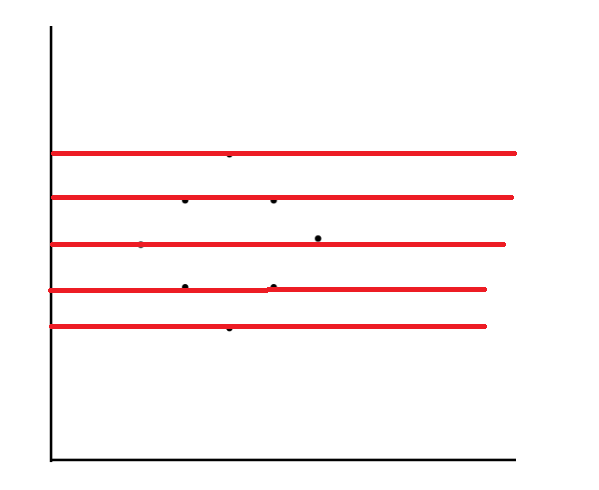
하한과 상한에서 직사각형의 y좌표를 조합을 구할 수 있습니다.

직선으로 표현하면 위와 같이 진행됩니다.
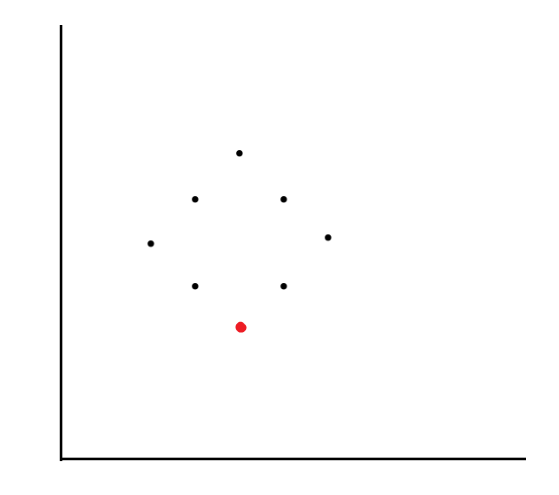
위 조합 사이에서 x의 좌표값의 개수를 구한 뒤 N/2개가 될 때 직사각형의 넓이를 구합니다.
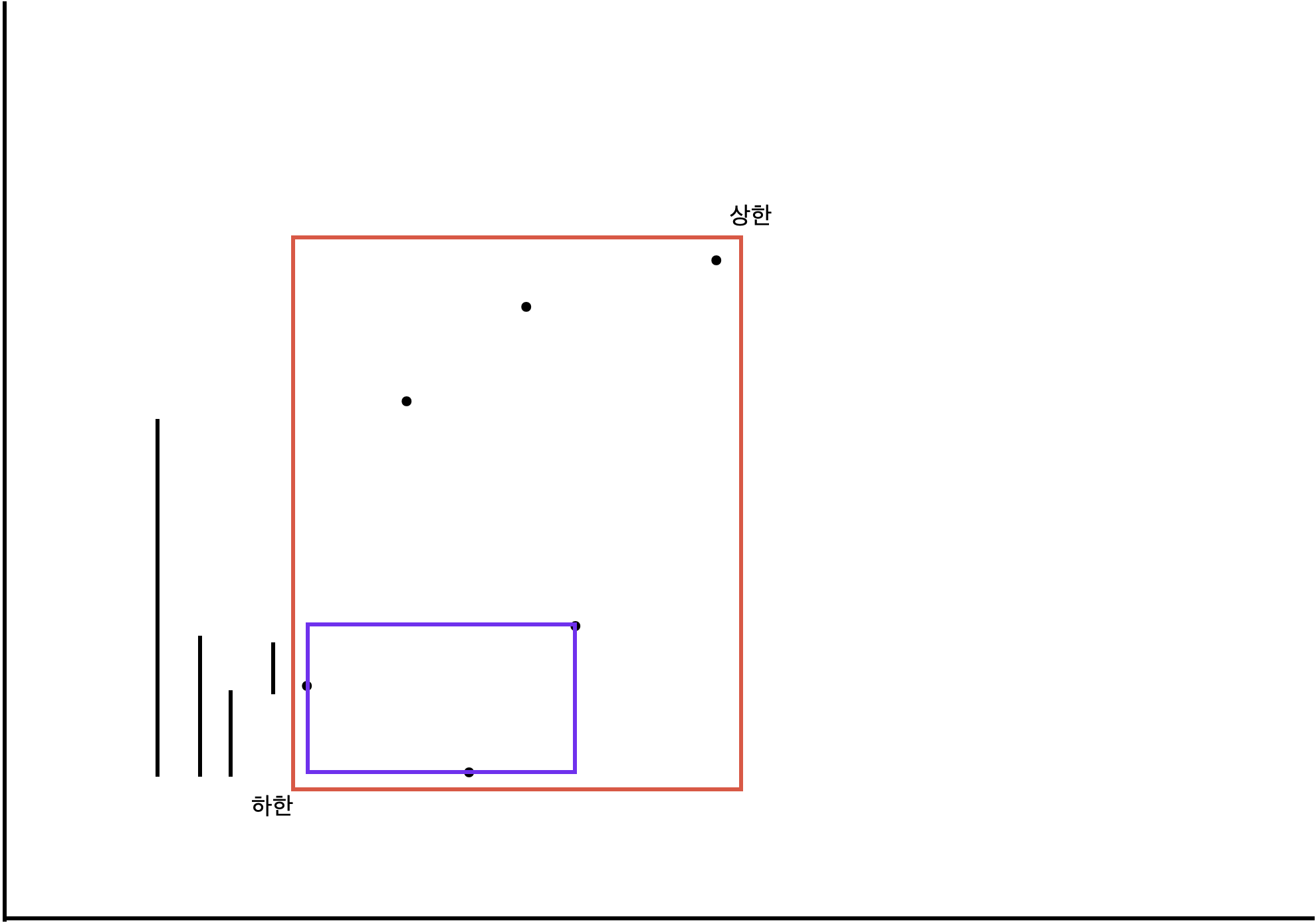
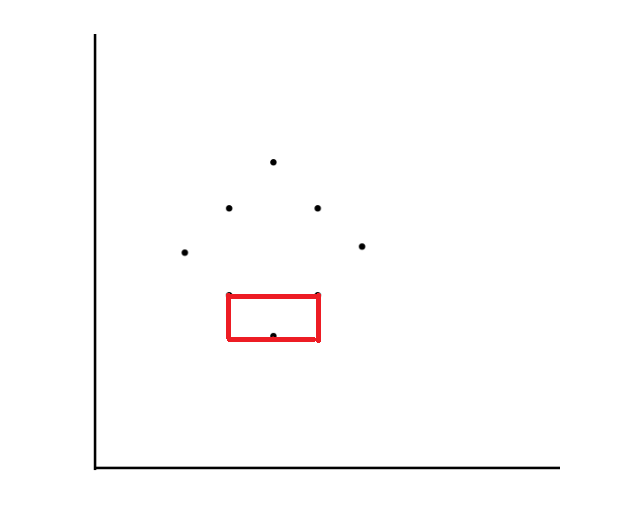
위와 같이 직사각형을 만들 수 있으며, 직사각형의 넓이를 구할 때에는 아래 점화식으로 구하게 됩니다.
maxY : y의 큰 값
minY : y의 작은 값
maxX : x의 큰 값
minX : x의 작은 값
직사각형의 넓이 : (maxY - minY + 2) X (maxX - minX)
여기서 각 +2를 진행하는 이유는 변에 포함되어 있는 점은 내부에 있는 것이 아니기 때문입니다.
즉, 만든 직사각형 하한에서 (x - 1, y - 1), 상한에서(x + 1, y + 1)을 진행하기 때문에 +2을 진행합니다.
위 과정에서 만들 수 있는 모든 직사각형을 탐색하여 직사각형의 최소 넓이를 구하면 됩니다.
※예제 입력 과정을 살펴보시면 이해하시기 편하실 것입니다.
예제입력 3.
1. 입력된 정보를 저장합니다.
N : 8
평면 좌표
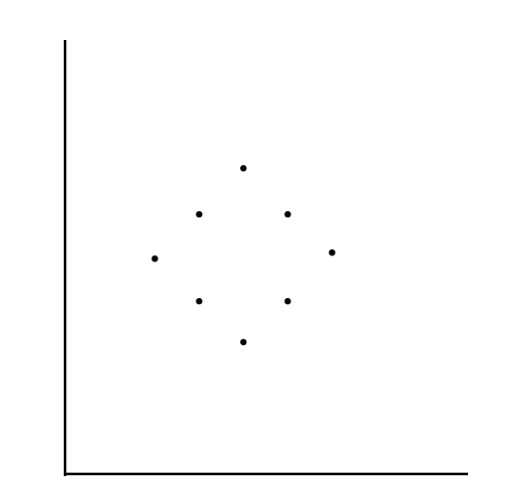
2. 좌표의 상한/하한을 기준으로 조건에 만족하는 모든 직사각형을 탐색합니다.
상한/하한 구분
직사각형 넓이가 될 수 있는 y좌표
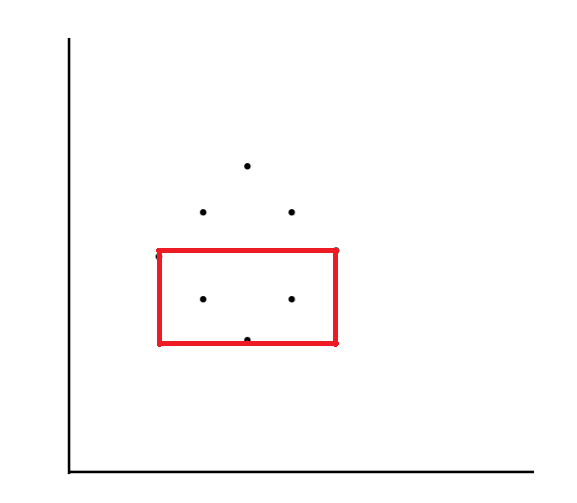
내부에 속한 x : { 5, 6, 7, 8, 9 }
{ 5, 6, 7, 8 } : 4개로 직사각형 만들기 가능
→ (7 - 5 + 2) × (8 - 5 + 2) = 4 × 5 = 20{ 6, 7, 8, 9 } : 4개로 직사각형 만들기 가능
→ (7 - 5 + 2) × (9 - 6 + 2) = 4 × 5 = 20
.....
(6, 8)일 때
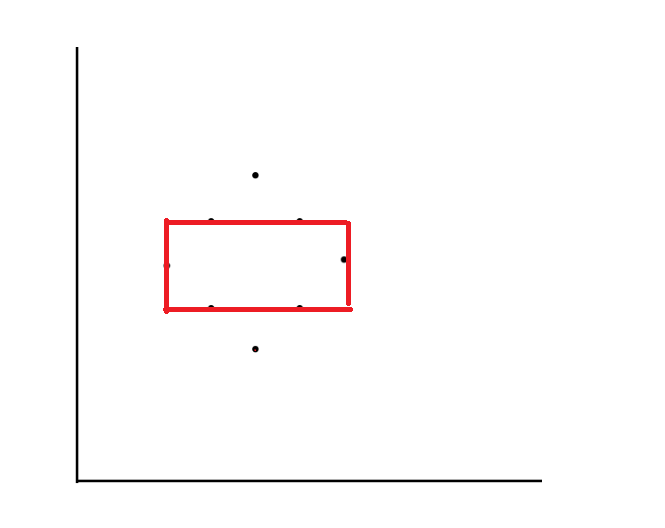
내부에 속한 x : { 5, 6, 6, 8, 8, 9 }
{ 5, 6, 6, 8 } : 4개로 직사각형 만들기 가능
→ (8 - 6 + 2) × (8 - 5 + 2) = 4 × 5 = 20
{ 6, 6, 8, 8 } : 4개로 직사각형 만들기 가능
→ (8 - 6 + 2) × (8 - 6 + 2) = 4 × 4 = 16
{ 6, 8, 8, 9 } : 4개로 직사각형 만들기 가능
→ (8 - 6 + 2) × (9 - 6 + 2) = 4 × 5 = 20
....
3. 탐색을 통해 얻은 최소 직사각형의 넓이를 결과로 출력합니다.
탐색이 끝났을 때, (6, 8)가 최소 직사각형의 넓이
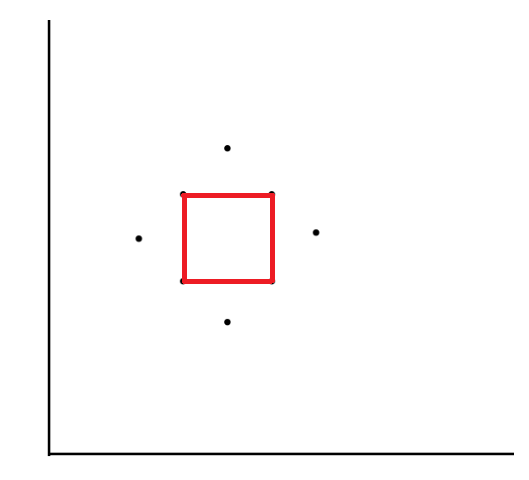
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 좌표의 정보를 띄어쓰기 기준 나누었습니다.
- 존재하는 y좌표를 기준으로 조합을 진행하여 존재하는 직사각형을 탐색합니다.
- Collections.sort()을 통해서 y좌표, x좌표를 정렬를 통해 직사각형의 넓이를 구합니다.
- 탐색을 진행하면서 직사각형의 넓이를 구하여 최소값을 탐색합니다.
- 탐색을 통해 얻은 최소 직사각형의 넓이를 결과로 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
결과코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
//좌표 정보 관련 클래스
static class Pos implements Comparable<Pos> {
int x, y;
Pos(int x, int y){
this.x = x;
this.y = y;
}
//좌표 y기준 오름차순 정렬, 동일할 때에는 x기준 오름차순 정렬
@Override
public int compareTo(Pos p) {
if(p.y == this.y){
return this.x - p.x;
}
return this.y - p.y;
}
}
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
StringTokenizer st;
List<Pos> posList = new ArrayList<>();
List<Integer> yList = new ArrayList<>();
boolean[] duplicationY = new boolean[10001];
//입력값 저장
for(int i=0;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
posList.add(new Pos(x, y));
}
//좌표 정렬 진행
Collections.sort(posList);
//중복되지 않은 y좌표 구하기
for(Pos cur : posList){
if(!duplicationY[cur.y]){
duplicationY[cur.y] = true;
yList.add(cur.y);
}
}
int len = yList.size();
int result = Integer.MAX_VALUE;
int halfN = N/2;
List<Integer> cur = new ArrayList<>();
//y좌표의 조합을 통해 모든 직사각형 탐색
for(int i=0;i<len;i++){
int idx = 0;
for(int j=i;j<len;j++){
int endY = yList.get(j);
//해당 y좌표 조합에서 포함된 x좌표들 구하기
while(idx < N && posList.get(idx).y <= endY){
if(yList.get(i) <= posList.get(idx).y){
cur.add(posList.get(idx).x);
}
idx++;
}
//x좌표의 개수가 N/2개가 이하일 때 : N/2개를 포함시킬 수 없음
if(cur.size() < halfN){
continue;
}
//x좌표 오름차순 정렬
Collections.sort(cur);
//직사각형 최소 넓이 비교하기
for(int k=0;k<=cur.size()-halfN;k++){
result = Math.min(result, (cur.get(k+halfN-1) - cur.get(k) + 2) * (endY - yList.get(i) + 2));
}
}
cur.clear();
}
//최소 직사각형의 넓이 BufferedWriter 저장
bw.write(String.valueOf(result));
bw.flush(); //결과 출력
bw.close();
br.close();
}
}'백준' 카테고리의 다른 글
| [백준, Java] 14224번, 작은 정사각형2, (이분 탐색) (0) | 2024.03.14 |
|---|---|
| [백준, Java] 2613번, 숫자구슬, (이분 탐색) (4) | 2024.03.05 |
| [백준, Java] 15912번, 우주선 만들기, (DP) (0) | 2024.02.08 |
| [백준, Java] 17307번, 색깔 통일하기, (누적합) (0) | 2024.02.06 |
| [백준, Java] 23758번, 중앙값 제거, (그리드) (1) | 2024.01.28 |




댓글