문제 링크
14284번: 간선 이어가기2
정점 n개, 0개의 간선으로 이루어진 무방향 그래프가 주어진다. 그리고 m개의 가중치 간선의 정보가 있는 간선리스트가 주어진다. 간선리스트에 있는 간선 하나씩 그래프에 추가해 나갈 것이다. 이때, 특정 정점 s와 t가 연결이 되는 시점에서 간선 추가를 멈출 것이다. 연결이란 두 정점이 간선을 통해 방문 가능한 것을 말한다...
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
이 문제에 핵심
1. n개의 간선과 0개의 간선 상태에서 m개의 간선이 순차적으로 추가될 예정입니다.
2. 각 간선에는 무방향이며 가중치가 존재합니다.
3. 추가되는 간선의 순서를 변경할 수 있을 때 s → t 으로 이동하는 간선치의 최소합을 결과로 출력합니다.
4. 모든 정점이 연결된 연결 그래프가 입력으로 주어집니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 다익스트라를 통해서 S → T으로 이동하는 최단 거리를 탐색합니다.
3. 탐색을 통해 얻은 최단 거리를 결과로 출력합니다.
최단 거리 구하기(그래프 탐색, 다익스트라)
이 문제에서 간선이 0개에서 m개씩 순차적으로 추가되고 순서를 바뀔 수 있다고 표현하고 있습니다.
→ 즉, 최단 거리를 가지는 간선치가 먼저 추가된다고 가정한다면 순서에 대해서는 신경쓰지 않아도 됩니다.
해당 문제는 주어진 정점과 간선을 이용해서 S → T으로 이동하는 가중치의 최소합을 결과로 출력하라는 뜻입니다.
즉, 다익스트라를 통해서 S → T으로 최단 거리를 구하라는 문제입니다.
예제입력 1.
1. 입력된 정보를 저장합니다.
S : 1
T : 8
정점 및 간선 정보
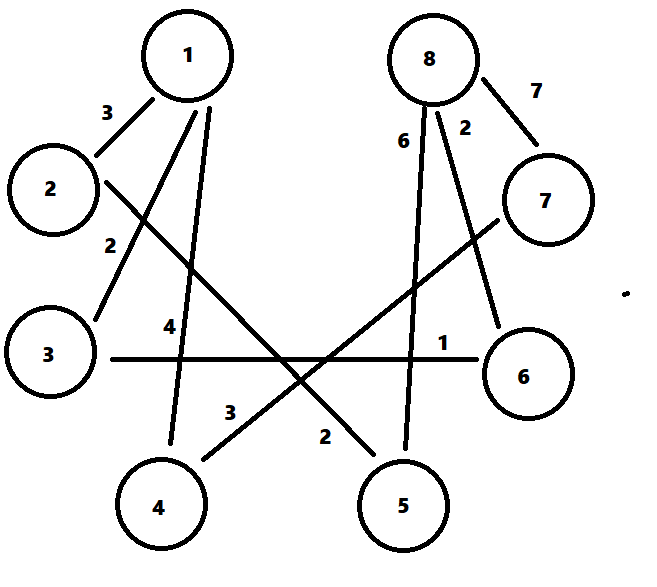
2. 다익스트라를 통해서 S → T으로 이동하는 최단 거리를 탐색합니다.
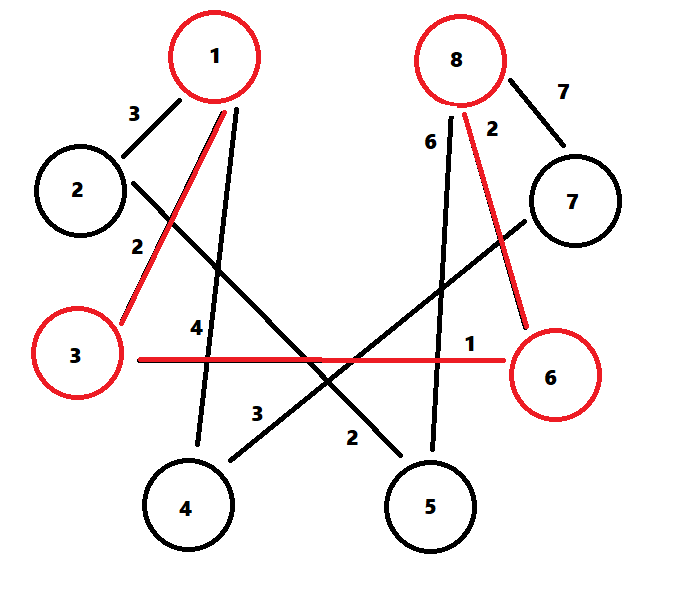
경로 : 1 → 3 → 6 → 8
가중치 합 : 2 + 1 + 2 = 5
3. 탐색을 통해 얻은 최단 거리를 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer을 이용해서 정점 및 간선의 정보를 띄어쓰기 기준 나누었습니다.
- dijkstra를 통해서 S에서 T까지 이동하는 최단 거리를 구합니다.
- 최단 거리를 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- dijkstra 함수는 다익스트라를 통해서 S에서 T까지 가는 최단 거리를 구합니다.
결과코드
import java.io.*;
import java.util.*;
public class Main {
//간선 및 Dijkstra에서 사용될 Node Class
static class Node implements Comparable<Node>{
//idx : 현재 인덱스, dist : 가중치
int idx, dist;
public Node(int idx, int dist) {
this.idx = idx;
this.dist = dist;
}
//가중치 기준 오름차순 정렬
@Override
public int compareTo(Node n) {
return this.dist - n.dist;
}
}
//간선 정보 저장하는 List
static List<List<Node>> graph = new ArrayList<>();
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedWriter
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
//정점 개수 및 간선 개수 저장
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
//간선 정보 저장할 List 초기화
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
//간선 정보 저장
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.get(a).add(new Node(b, c));
graph.get(b).add(new Node(a, c));
}
//시작 정점, 종점 정점 저장
st = new StringTokenizer(br.readLine(), " ");
int s = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
//다익스트라를 진행하여 최단 거리 구하기
int answer = dijkstra(s, t, n);
//최단 거리 BufferedWriter 저장
bw.write(String.valueOf(answer));
bw.flush();
bw.close();
br.close();
}
//다익스트라를 통해서 s에서 t까지 최단 거리 구하는 함수
static int dijkstra(int start, int end, int n){
//다익스트라 세팅
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start, 0));
int[] dist = new int[n+1];
//최대값으로 설정
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
//다익스트라 진행
while(!pq.isEmpty()){
Node cur = pq.poll();
if(dist[cur.idx] < cur.dist){
continue;
}
//현재 정점에서 연결된 간선 탐색
for(Node next : graph.get(cur.idx)){
int cost = cur.dist + next.dist;
if(cost < dist[next.idx]){
dist[next.idx] = cost;
pq.add(new Node(next.idx, cost));
}
}
}
//t의 최단 거리 반환
return dist[end];
}
}'백준' 카테고리의 다른 글
| [백준, Java] 18513번, 샘터(그래프 탐색) (1) | 2024.10.24 |
|---|---|
| [백준, Java] 16211번, 백채원(그래프 탐색, 다익스트라) (3) | 2024.10.12 |
| [백준, Java] 2251번, 물통(그래프 탐색) (2) | 2024.09.17 |
| [백준, Java] 1943번, 동전 분배(DP) (0) | 2024.08.09 |
| [백준, Java] 25417번, 고속의 숫자 탐색(BFS) (0) | 2024.08.01 |




댓글