문제 링크
23353번: 승부 조작
고양이 랑이와 메리는 오목 게임의 변형인 냥목 게임을 하고 있다. 냥목 게임의 규칙은 복잡하니 점수 계산 방법만 보자...
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
이 문제에 핵심
1. N × N 크기의 바둑판이 존재하며 흑돌, 백돌이 놓여져 있습니다.
2. 점수는 가로, 세로, 대각선 중 하나의 방향으로 연속하여 존재하는 가장 긴 흑돌의 길이입니다.
3. 백돌 1개를 흑돌로 바꿀 수 있을 때 최대 점수를 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 백돌을 흑돌로 변경하는 경우를 DP(점화식)을 통해서 탐색합니다.
3. 탐색으로 얻은 최대 점수를 결과로 출력합니다.
최대 점수 구하기(DP)
가로, 세로, 대각선으로 연속하는 흑돌이 길이가 점수가 됩니다.

각 방향의 흰돌을 흑돌로 바꾸는 것에 대해서 영향을 받지 않습니다.
그러면 이제, 돌의 유형에 따라 점수가 어떻게 접근되는지 확인하겠습니다.
비어있는 위치 : 0
절대로 흑돌과 연결되지 않기 때문에 해당 위치에 점수는 항상 0점입니다.
흑돌의 위치 : 1
항상 점수로 계산되기 때문에 현재 방향의 이전 값 + 1
백돌의 위치 : 2
백돌을 그대로 사용할 때 해당 위치는 항상 0점입니다.
백돌을 흑돌로 바꾸어서 사용할 때에는 현재 방향의 이전 값 + 1
아래는 예시 바둑판
| 0 | 1 | 1 |
| 0 | 2 | 2 |
| 1 | 0 | 0 |
다이나믹 프로그래밍 테이블로 살펴보면 아래와 같습니다.
DP[i][j][k][s] = 바둑판 (i, j) 위치의 k(0 : 백돌 → 흑돌 변경 X, 1 : 백돌 → 흑돌 변경 O)일 때 s(→, ↓, ↘, ↙)방향의 최대 점수
| 0 ([0, 0, 0, 0], [0, 0, 0, 0]) | 1 ([1, 1, 1, 1], [1, 1, 1, 1]) | 1 ([2, 1, 1, 1], [2, 1, 1, 1]) |
| 0 ([0, 0, 0, 0], [0, 0, 0, 0]) | 2 ([0, 0, 0, 0], [1, 2, 1, 2]) | 2 ([0, 0, 0, 0], [1, 2, 2, 1]) |
| 1 ([1, 1, 1, 1], [1, 1, 1, 1]) | 0 ([0, 0, 0, 0], [0, 0, 0, 0]) | 0 ([0, 0, 0, 0], [0, 0, 0, 0]) |
위 테이블을 기반으로 점화식을 살펴보면
바둑판 위치의 유형
비어있는 위치 : 0
([0, 0, 0, 0], [0, 0, 0, 0]) : 점수를 얻을 수 없음
흑돌의 위치 : 1
DP[i][j][k][0] = DP[i][j-1][k][0] + 1;
DP[i][j][k][1] = DP[i-1][j][k][1] + 1;
DP[i][j][k][2] = DP[i-1][j-1][k][2] + 1;
DP[i][j][k][3] = DP[i-1][j+1][k][3] + 1;
백돌의 위치 : 2
DP[i][j][0][s] = [0, 0, 0, 0]
DP[i][j][1][0] = DP[i][j-1][k][0] + 1;
DP[i][j][1][1] = DP[i-1][j][k][1] + 1;
DP[i][j][1][2] = DP[i-1][j-1][k][2] + 1;
DP[i][j][1][3] = DP[i-1][j+1][k][3] + 1;
점화식은 이전의 탐색했던 방향의 값을 기준으로 현재 바둑판 돌 유형에 따른 값들을 갱신해서 중복하는 탐색을 방지하고 있습니다.
점화식을 탐색하면서 발생하는 점수 중 가장 큰 값을 결과로 출력하면 됩니다.
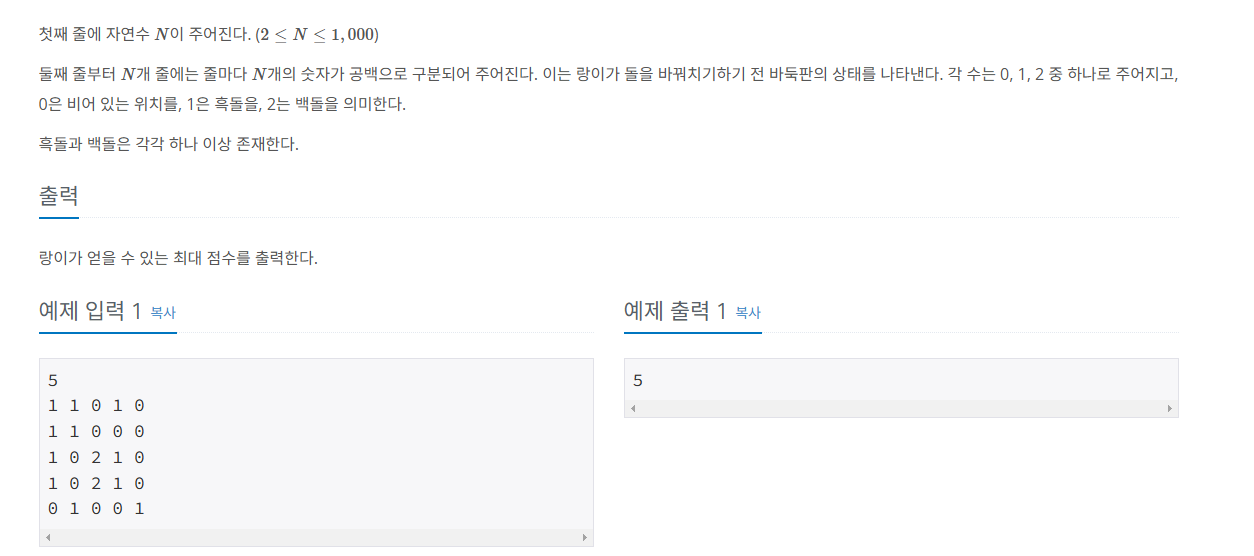
예제입력 1.
1. 입력된 정보를 저장합니다.
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 2 | 1 | 0 |
| 1 | 0 | 2 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
2. 백돌을 흑돌로 변경하는 경우를 DP(점화식)을 통해서 탐색합니다.
점화식을 기준 다이나믹 프로그래밍 테이블로 살펴보면 아래와 같습니다.
| [1, 1, 1, 1], [1, 1, 1, 1] | [2, 1, 1, 1], [1, 1, 1, 1] | [0, 0, 0, 0], [0, 0, 0, 0] | [1, 1, 1, 1], [1, 1, 1, 1] | [0, 0, 0, 0], [0, 0, 0, 0] |
| [1, 2, 1, 2], [1, 2, 1, 2] | [2, 2, 2, 1], [2, 2, 2, 1] | [0, 0, 0, 0], [0, 0, 0, 0] | [0, 0, 0, 0], [0, 0, 0, 0] | [0, 0, 0, 0], [0, 0, 0, 0] |
| [1, 3, 1, 2], [1, 3, 1, 2] | [0, 0, 0, 0], [0, 0, 0, 0] | [0, 0, 0, 0], [1, 1, 3, 1] | [1, 1, 1, 1], [2, 1, 1, 1] | [0, 0, 0, 0], [0, 0, 0, 0] |
| [1, 4, 1, 1], [1, 4, 1, 1] | [0, 0, 0, 0], [0, 0, 0, 0] | [0, 0, 0, 0], [1, 1, 1, 2] | [1, 2, 1, 1], [2, 2, 4, 1] | [0, 0, 0, 0], [0, 0, 0, 0] |
| [0, 0, 0, 0], [0, 0, 0, 0] | [1, 1, 2, 1], [1, 1, 2, 2] | [0, 0, 0, 0], [0, 0, 0, 0] | [0, 0, 0, 0], [0, 0, 0, 0] | [1, 1, 2, 1], [1, 1, 5, 1] |
테이블의 최대값 : DP[5][5][1][2]
- (5, 5)위치의 ↘ 방향으로 백돌을 흑돌로 바꾸었을 때 최대 점수
3. 탐색으로 얻은 최대 점수를 결과로 출력합니다
테이블의 최대 값 : DP[5][5][1][2] = 5
5을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer을 통해서 바둑판의 정보를 띄어쓰기 기준 나누었습니다.
- 바둑판 위치 유형에 따라 cal함수를 통해 DP[][][][]을 탐색합니다.
- DP[][][][] 탐색으로 얻은 최대값을 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- cal함수는 →, ↓, ↘, ↙ 방향 순으로 점화식을 계산하는 하며, 그에 따른 최대값을 반환합니다.
결과코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
class Main {
static int[][][][] DP;
public static void main(String[] args) throws Exception {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
StringTokenizer st;
int[][] board = new int[n+2][n+2];
//바둑판 정보 저장
for(int i=1;i<=n;i++){
st = new StringTokenizer(br.readLine()," ");
for(int j=1;j<=n;j++){
board[i][j] = Integer.parseInt(st.nextToken());
}
}
int max = 0;
DP = new int[n+2][n+2][2][4];
//바둑판 유형에 따른 점화식 적용
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
//흰돌일 때
if(board[i][j] == 1){
int nonBlackMax = cal(i, j, 0, 0);
int useBlackMax = cal(i, j, 1, 1);
max = Math.max(max, Math.max(nonBlackMax, useBlackMax));
}else if(board[i][j] == 2){ //흑돌일 때
int useBlackMax = cal(i, j, 1, 0);
max = Math.max(max, useBlackMax);
}
}
}
//DP 테이블 최대값 BufferedWriter 저장
bw.write(String.valueOf(max));
bw.flush(); //결과 출력
bw.close();
br.close();
}
//점화식 적용하는 함수
static int cal(int row, int col, int target, int blackUse){
//→, ↓, ↘, ↙ 방향순으로 점화식 적용
DP[row][col][target][0] = DP[row][col-1][blackUse][0] + 1;
DP[row][col][target][1] = DP[row-1][col][blackUse][1] + 1;
DP[row][col][target][2] = DP[row-1][col-1][blackUse][2] + 1;
DP[row][col][target][3] = DP[row-1][col+1][blackUse][3] + 1;
//점화식 이후 최대값 반환
return Math.max(DP[row][col][target][0], Math.max(DP[row][col][target][1], Math.max(DP[row][col][target][2], DP[row][col][target][3])));
}
}'백준' 카테고리의 다른 글
| [백준, Java] 17609번, 회문(투 포인터) (0) | 2025.03.24 |
|---|---|
| [백준, Java] 7570번, 줄 세우기(그리드, DP) (0) | 2025.01.07 |
| [백준, Java] 2698번, 인접한 비트의 개수(DP) (0) | 2024.12.10 |
| [백준, Java] 23829번,인물예술탐사주간(누적합) (0) | 2024.12.05 |
| [백준, Java] 2374번, 같은 수로 만들기(스택, 그리드) (0) | 2024.11.19 |




댓글