문제 링크
17396번: 백도어
유섭이는 무척이나 게으르다. 오늘도 할 일을 모두 미뤄둔 채 열심히 롤을 하던 유섭이는 오늘까지 문제를 내야 한다는 사실을 깨달았다. 그러나 게임은 시작되었고 지는 걸 무척이나 싫어하는 유섭이는 어쩔 수 없이 백도어를 해 게임을 최대한 빠르게 끝내기로 결심하였다.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명


접근 방법
이 문제에 핵심
1. N개의 분기점이 존재하고, M개의 분기점을 잇는 길이 존재합니다.
2. M개의 길은 양방향이며, t만큼의 시간이 걸리게 됩니다.
3. 0번 분기점에서 N-1번 분기점까지 도착하는 최소 시간을 구해야 합니다.
4. 각 분기점의 방문 가능 여부(0 : 방문 가능, 1 : 불가능)에 따라 접근 여부가 결정됩니다.
5. N-1번 분기점은 도착지이면서 넥서스이기 때문에 항상 방문 가능 여부는 1입니다.
6. 0번에서 N-1까지의 최단 시간을 결과로 출력하며, 도달하지 못할 경우 -1을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 0번 분기점에서 N-1번 분기점까지의 최단 시간을 탐색합니다.
3. 탐색을 통해 얻은 최단 시간을 결과로 출력합니다.
최단 시간 탐색(다익스트라)
다음 분기점으로 가기 위해서는 N-1번째 분기점을 제외하고는 방문 가능 여부가 0이어야 한다.
또한, 각 분기점 길에 따라 걸리는 시간이 다르기 때문에 배열을 통해서 최단 시간을 관리합니다.
| 분기점1 | 분기점2 | 분기점3 | |
| 최단 시간 | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE |
위 배열처럼 최단 시간 값을 매우 큰 값으로 설정한 뒤에 최단 시간을 순차적으로 탐색하여 처리합니다.
▶︎ Long.MAX_VALUE인 이유는 100,000 x 100,000 으로 정수(int)형을 벗어날 수 있습니다.
각 분기점에 대해서 이어진 길을 탐색하며, 해당 길을 통해 다음 분기점으로 이동하였을 경우 최단 시간이 되지 않으면 해당 길을 이용하지 않도록 합니다.
예제입력 1.
1. 입력된 정보를 저장합니다.
초록 : 방문 가능
노랑 : 방문 불가능

2. 0번 분기점에서 N-1번 분기점까지의 최단 시간을 탐색합니다.
먼저 최단 시간을 설정합니다.
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE |
0번 분기점에서 시작하므로, 분기점 0은 항상 최단 시간이 0입니다.
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | 0 | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE | Long.MAX_VALUE |
0번 분기점부터 다익스트라 탐색을 통해서 최단 시간을 탐색합니다.

0번 분기점 ▶︎ 1번 분기점 : 7
- Long.MAX_VALUE보다 작기 때문에 최단 시간 변경
0번 분기점 ▶︎ 2번 분기점 : 2
- Long.MAX_VALUE보다 작기 때문에 최단 시간 변경
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | 0 | 7 | 2 | Long.MAX_VALUE | Long.MAX_VALUE |
현재 Queue : {1번 분기점, 2번 분기점} - 최단 시간을 갖은 2번 분기점 탐색 진행
2번 분기점 기준 최단 시간을 탐색합니다.
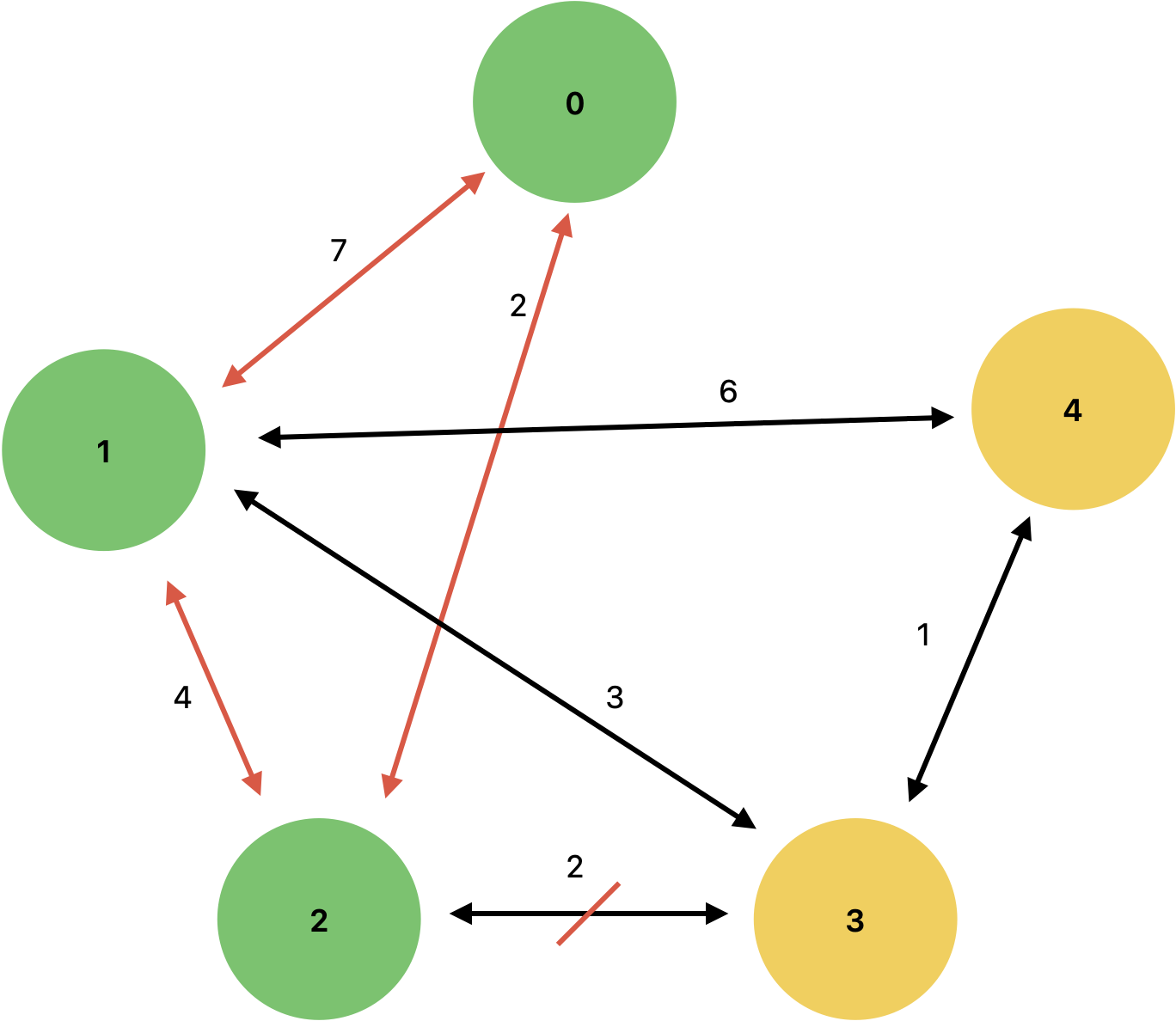
2번 분기점 ▶︎ 3번 분기점 : X
- 방문 가능하지 않기 때문에 접근 불가!
2번 분기점 ▶︎ 1번 분기점 : 2 + 4 = 6
- 7보다 작기 때문에 최단 시간 변경
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | 0 | 6 | 2 | Long.MAX_VALUE | Long.MAX_VALUE |
현재 Queue : {1번 분기점} - 최단 시간를 갖은 1번 분기점 탐색 진행
1번 분기점 기준 최단 시간을 탐색합니다.
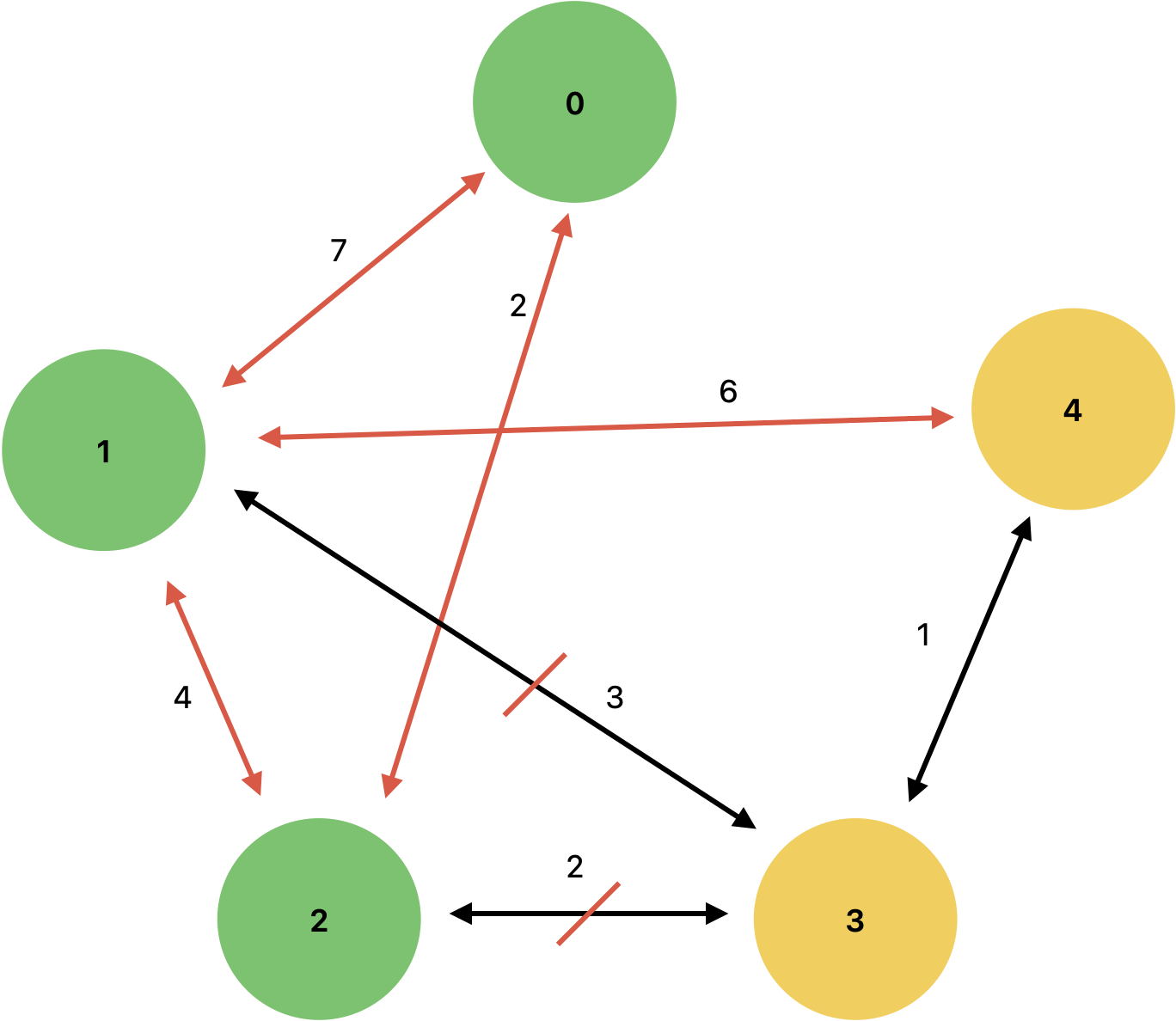
1번 분기점 ▶︎ 3번 분기점 : X
- 방문 가능하지 않기 때문에 접근 불가!
1번 분기점 ▶︎ 4번 분기점 : 2 + 4 + 6 = 12
- Long.MAX_VALUE보다 작기 때문에 최단 시간 변경
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | 0 | 6 | 2 | Long.MAX_VALUE | 12 |
목표 N-1번 분기점에 도착
현재 Queue : {} - 모든 거리 탐색 완료!
3. 탐색을 통해 얻은 최단 시간를 결과로 출력합니다.
| 분기점0 | 분기점1 | 분기점2 | 분기점3 | 분기점4 | |
| 최단시간 | 0 | 6 | 2 | Long.MAX_VALUE | 12 |
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer을 통해 분기점 정보를 띄어쓰기 기준 나누었습니다.
- 방문 여부 및 분기점 정보으로 seach함수를 통해서 최단 시간을 탐색합니다.
- 탐색으로 얻은 최단 시간을 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
- search함수는 다익스트라를 통해서 0번 분기점에서 N-1번까지의 최단 시간을 탐색합니다.
결과코드
import java.util.*;
import java.io.*;
public class Main {
//분기점을 잇는 길 정보(nxt : 이동하려는 분기점, distance : 시간)
static class Node{
int nxt;
int distance;
public Node(int nxt, int distance) {
this.nxt = nxt;
this.distance = distance;
}
}
//다익스트라 탐색에 대한 정보(current : 현재 분기점, distance : 사용 시간)
static class Pos implements Comparable<Pos>{
int current;
long distance;
public Pos(int current, long distance) {
this.current = current;
this.distance = distance;
}
//정렬 조건(사용 시간 오름차순 정렬)
@Override
public int compareTo(Pos pos) {
if(this.distance > pos.distance){
return 1;
}else if(this.distance == pos.distance){
return 0;
}
return -1;
}
}
public static void main(String[] args) throws IOException {
//입력값 설정하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine(), " ");
int[] movable = new int[n];
//방문 가능 여부 정보 저장
for(int i=0;i<n;i++){
movable[i] = Integer.parseInt(st.nextToken());
}
List<List<Node>> graph = new ArrayList<>();
for(int i=0;i<n;i++){
graph.add(new ArrayList<>());
}
//분기점 잇는 길 양방향 정보 저장
for(int i=0;i<m;i++){
st= new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
graph.get(a).add(new Node(b, d));
graph.get(b).add(new Node(a, d));
}
//최단 시간 구하기
long answer = search(graph, movable, n);
//최단 시간 BufferedWriter 저장
bw.write(String.valueOf(answer));
bw.flush(); //결과 출력
bw.close();
br.close();
}
//다익스트라 탐색을 통한 최단 시간 구히기
static long search(List<List<Node>> graph, int[] movable, int n){
//걸린 시간 오름차순 기준 분기점 관리하는 우선순위 큐
PriorityQueue<Pos> pq = new PriorityQueue<>();
//0번 분기점 시작 위치로 설정
pq.add(new Pos(0, 0L));
//최단 시간 설정
long[] minDistance = new long[n];
Arrays.fill(minDistance, Long.MAX_VALUE);
//시작 위치는 최단 시간 0으로 설정
minDistance[0] = 0;
//다익스트라 탐색 진행
while(!pq.isEmpty()){
Pos curPos = pq.poll();
//현재 걸린 시간이 최단보다 큰 경우 탐색 넘기기
if(curPos.distance > minDistance[curPos.current]) {
continue;
}
//현재 분기점 기준 이어진 길 탐색
for(Node nxt : graph.get(curPos.current)){
long nxtDistance = nxt.distance + curPos.distance;
if(!(nxt.nxt < n-1 && movable[nxt.nxt] == 1) && minDistance[nxt.nxt] > nxtDistance){
minDistance[nxt.nxt] = nxtDistance;
pq.offer(new Pos(nxt.nxt, nxtDistance));
}
}
}
//최단 시간 반환
return minDistance[n-1] == Long.MAX_VALUE ? -1 : minDistance[n-1];
}
}'백준' 카테고리의 다른 글
| [백준, Java] 1245번, 농장관리(BFS) (0) | 2026.01.02 |
|---|---|
| [백준, Java] 3980번, 선발 명단(완전 탐색, 백트래킹) (0) | 2025.12.12 |
| [백준, Java] 3067번, Coins(DP) (0) | 2025.11.03 |
| [백준, Java] 2343번, 기타 레슨( 이분 탐색) (0) | 2025.10.10 |
| [백준, Java] 2666번, 벽장문이 이동(DP) (0) | 2025.09.18 |




댓글