문제 링크
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
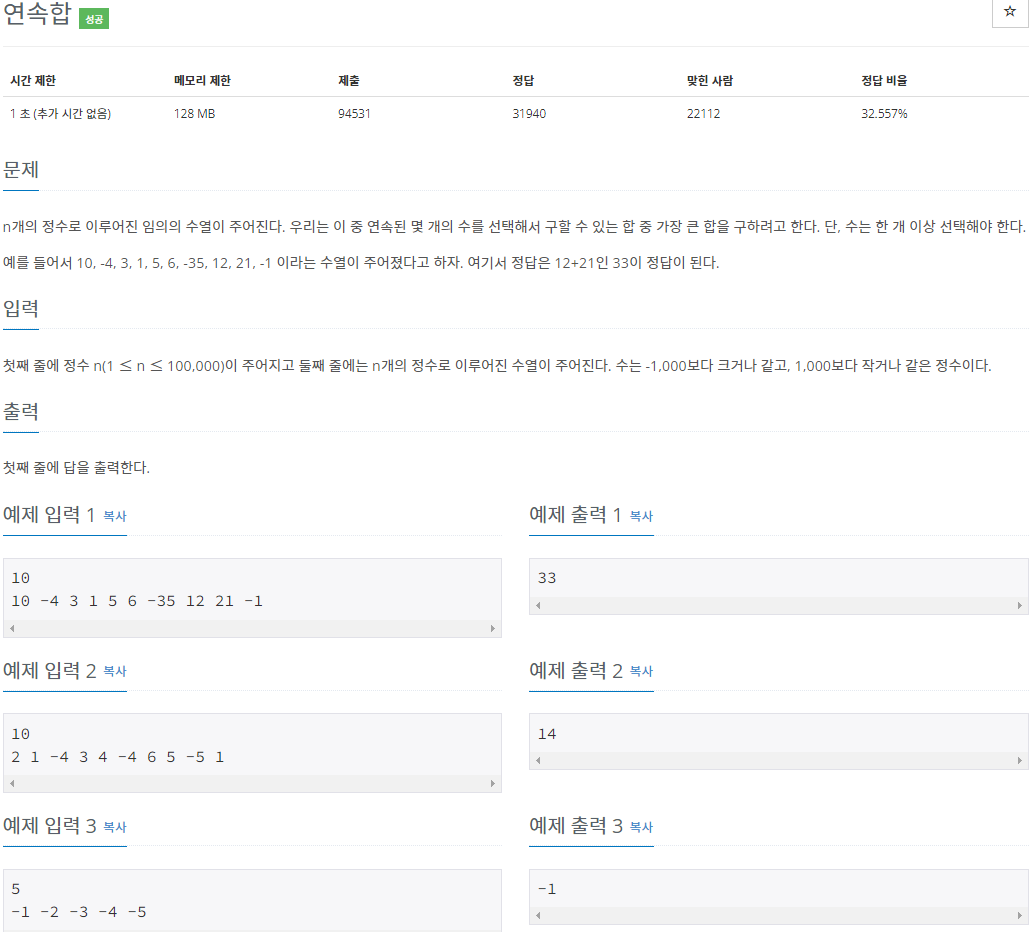
접근 방법
동적계획법이란 위 문제와 같이 동일한 연산을 계속 반복하여 비효율적으로 코드가 실행되어 그것을 향상시키기 위하여반복되는 연산의 결과를 따로 저장하여 적재적소에 코드가 더 효율적으로 만드는 방법입니다.
연속된 합에서 마지막 수는 자기자신이 최대수로 표현할 수 있습니다.
예제 입력 1에 대하여 연속합에 표를 만들면
| 10 | -4 | 3 | 1 | 5 | 6 | -35 | 12 | 21 | -1 |
| 21 | 11 | 15 | 12 | 11 | 6 | -2 | 33 | 21 | -1 |
표를 보면 규칙을 발견할 수 있습니다.
자신의 숫자에서 뒤에 나오는 숫자의 연속합에 최대값과 더하였을 때 더 커지면 더하고 크지 않는다면 자기 자신의 숫자가 최대값이 되는 것입니다.
Math.max(자기자신 숫자, 뒤에 숫자 연속합 최대값 + 자기자신 숫자)
예를 들어 -35일 때 Math.max(-35, -35 + 33) = -2로 -35에 연속합 최대값이 -2가 됩니다.
숫자에 0이 들어갈 수 있어서 int형식의 배열로 진행한다면 다른 수로 초기화를 진행해주어야 하기 때문에 Integer를 사용하여 메모이제이션을 선언하였습니다.
숫자에 따른 연속합 최대값을 저장하기 위해 [숫자 수+1]로 배열의 메모이제이션을 구성하였습니다.
- 연속합 최대값을 저장할 메모이제이션 배열 check를 만들었습니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- 연속값을 계산하는함수 sum을 만들었습니다.
- for문을 통하여 메모이제이션에 저장된 연속합의 최대값을 구하기 위해 Math.max 이용하였습니다.
- System.out.println을 사용하여 연속합의 최대값을 출력하였습니다.
- 메모이제이션이 null인 경우는 그 수의 연속합이 저장되어 있지 않다고 판단하여 재귀를 실행
- check가 null이 아니면 탐색된 값이기 때문에 메모이제이션에 값을 가져온다.
- 재귀를 이용하여 위에 알고리즘처럼 작동하게 sum함수를 작성하였습니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
static Integer[] check; //메모이제이션
static int[] num; //숫자 저장
static int index; //숫자 수
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//BufferedReader를 통해 입력 값 받기
//---------입력값 저장 및 배열 초기화---------
index = Integer.parseInt(br.readLine());
check = new Integer[index+1];
num = new int[index+1];
StringTokenizer st = new StringTokenizer(br.readLine()," ");
int max = Integer.MIN_VALUE;
for(int i=1;i<=index;i++)
num[i] = Integer.parseInt(st.nextToken());
check[index] = num[index];
sum(1); //함수 실행
for(int i=index;i>0;i--) //최대값 구하기
max = Math.max(max, check[i]);
System.out.println(max); //결과 출력
br.close();
}
//---------연속합 구하는 함수----------
public static Integer sum(int depth) {
if(depth==index)
return check[index];
if(check[depth]==null) {
check[depth] = Math.max(num[depth], sum(depth+1) + num[depth]);
}
return check[depth];
}
}'백준' 카테고리의 다른 글
| [백준] 단계별로 풀어보기(단계:16,그리디 알고리즘,JAVA)11047번, 동전 0 (0) | 2022.01.31 |
|---|---|
| [백준] 단계별로 풀어보기(단계:15,동적계획법1,JAVA)12865번, 평범한 배낭 (0) | 2022.01.31 |
| [백준] 단계별로 풀어보기(단계:15,동적계획법1,JAVA)9251번, LCS (0) | 2022.01.28 |
| [백준] 단계별로 풀어보기(단계:15,동적계획법1,JAVA)2565번, 전깃줄 (0) | 2022.01.28 |
| [백준] 단계별로 풀어보기(단계:15,동적계획법1,JAVA)11054번, 가장 긴 바이토닉 부분 수열 (0) | 2022.01.28 |





댓글