상황
- 알고리즘 문제에서 주어진 선택지에서 몇 가지를 선택하도록 하는 경우가 많이 있습니다.
- 단순한 for문으로 재귀를 진행한다면 시간초과가 발생할 수 있습니다.
- 그래서 단순 for문, 메모이제이션을 사용한 동적계획법 등을 사용하여 알아보도록 하겠습니다.
이항계수란?
먼저 이항계수에 대하여 알아보도록 하겠습니다.내용은 아래 링크 위키백과에서 참조하여 작성하였습니다.
https://ko.wikipedia.org/wiki/%EC%9D%B4%ED%95%AD_%EA%B3%84%EC%88%98
이항 계수 - 위키백과, 우리 모두의 백과사전
조합론에서, 이항 계수(二項係數, 영어: binomial coefficient)는 이항식을 이항 정리로 전개했을 때 각 항의 계수이며, 주어진 크기의 (순서 없는) 조합의 가짓수이다. 자연수 n {\displaystyle n} 및 정수 k
ko.wikipedia.org
이항 계수를 간단하게 설명하면 여러 선택지 중 몇 개를 선택할 때 생기는 경우의 수입니다.
예를 들어 색이 다른 구슬 4개 중에 2개를 선택할 때 생기는 경우의 수 => 이항계수
이항계수를 표현하는 방법으로 nCm(n=선택지,m=선택할 수)로 위에 예는 ₄C₂로 표현할 수 있습니다.
다른 표현 방법으로 아래 그림처럼 표현할 수 있습니다.

n!/m!(n-m)! 0≤k≤n
0 k<0
0 k>n
이항 계수를 구하는 기본적인 공식입니다.
위의 예를 공식으로 표현하면
₄C₂ = 4!/2!(4-2)! = (4×3×2×1)/(2×1)(2×1) = 6
이항 계수의 값들을 표현하는 표가 존재합니다. = 파스칼의 삼각형

위에서부터 이행계수로 표현하면



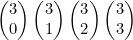
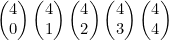
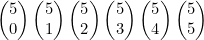
파스칼 삼각형을 보면 규칙을 찾을 수 있습니다.
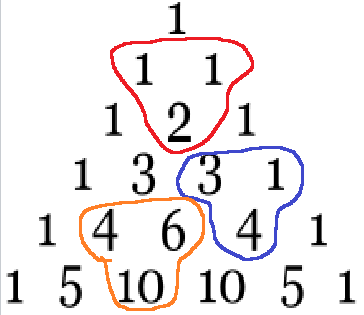
빨간색은 1 + 1 = 2
파란색은 3 + 1 = 4
주황색은 4 + 6 = 10
규칙은
nCm = n-₁Cm-₁ + n-₁Cm 으로
JAVA 배열에 대한 알고리즘으로 표현하면
num[n][m] = num[n-1][m-1] + num[n-1][m]을 구하는 식으로 사용하였습니다.
더 자세한 내용은 위에 위키백과 링크를 확인해주시면 감사하겠습니다.
사용법
단순 반복
import java.io.*;
import java.util.*;
public class Test{
static int N,K; //선택지, 선택수
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//BufferedReader를 통해 입력 값 받기
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//BufferedWriter를 통해 결과 값 출력
//--------입력값 저장-------------
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
int result = binomialCoefficient(N,K); //함수 실행
bw.write(result + "\n"); //결과 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//--------이항 계수 구하는 함수----------
public static int binomialCoefficient(int N, int K) {
int result = factorial(N)/(factorial(K)*factorial(N-K));
return result;
}
//----------팩토리얼 함수----------
public static int factorial(int n) {
if(n==1 || n==0)
return 1;
return n * factorial(n-1);
}
}기본적인 이항계수 공식을 그대로 알고리즘으로 표현한 방식입니다.
n!/m!(n-m)!을 그대로 구현한 것으로 이 알고리즘의 문제점은 시간복잡도가 높아서
알고리즘 문제를 해결할 때 시간초과를 발생할 확률이 매우 높습니다.
약분을 진행한 후 연산
import java.io.*;
import java.util.*;
public class Test{
static int N,K;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//BufferedReader를 통해 입력 값 받기
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//BufferedWriter를 통해 결과 값 출력
//----------입력 값 저장------------
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
int result = binomialCoefficient(N,K); //함수 실행
bw.write(result + "\n"); //결과 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//--------이항 계수 구하는 함수----------
public static int binomialCoefficient(int N, int K) {
int result = 1;
int temp = N-K;
for(int i=temp+1;i<=N;i++) {
result = result * i;
result = result / (i-temp);
}
return result;
}
}이 알고리즘은 모든 팩토리얼에 값을 구한 뒤 연산하는 것이 아닌 약분을 진행한 뒤 연산을 진행하는 것입니다.
n!/m!(n-m)!에서 n!을 n*....*(n-m+1)*(n-m)!으로 표현할 수 있습니다.
(n-m)!을 무조건 약분할 수 있기 때문에 식을
n*....*(n-m+1)/m!으로 표현할 수 있습니다.
이걸 알고리즘으로 표현하였습니다.
이 알고리즘에서도 문제를 해결할 때 단순 연산 코드보다는 시간복잡도가 좋지만 시간초과가 발생할 수 있습니다.
파스칼 삼각형과 메모이제이션을 이용한 동적계획법
import java.io.*;
import java.util.*;
public class Test{
static Integer num[][]; //메모이제이션 배열
static int N,K; //입력 값
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//BufferedReader를 통해 입력 값 받기
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//BufferedWriter를 통해 결과 값 출력
//----------입력값 저장 및 배열 초기화-----
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
num = new Integer[N+1][N+1];
int result = binomialCoefficient(N,K); //함수 실행
bw.write(result + "\n"); //결과 BufferedWriter에 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//----------이항 계수 구하는 함수---------
public static int binomialCoefficient(int N, int K) {
if(K==0 || N==K)
return 1;
if(num[N][K]==null)
num[N][K] = binomialCoefficient(N-1, K-1) + binomialCoefficient(N-1, K);
return num[N][K];
}
}이 코드는 메모이제이션을 이용하여 동적계획법으로 작성한 코드로 파스칼 삼각형에서 얻은 규칙을 이용하여 작성되었습니다.
메모이제이션에는 파스칼 삼각형의 값들이 들어가야 하기 때문에 크기를 N+1만큼 만들었습니다. => num[N+1][N+1]
위에서 나온 규칙의 알고리즘을
num[n][m] = num[n-1][m-1] + num[n-1][m]을 재귀하는 형식
=> num[N][K] = binomialCoefficient(N-1, K-1) + binomialCoefficient(N-1, K)
현재까지는 문제를 풀면서 시간초과는 발생하지 않았습니다.
문제
이항 계수 관련한 백준 온라인 문제를 해결한 링크를 첨부하겠습니다.
https://tussle.tistory.com/283?category=972975
[백준] 단계별로 풀어보기(단계:17,정수론 및 조합론,JAVA)1010번, 다리놓기
문제 링크 1010번: 다리 놓기 www.acmicpc.net 주의사항 JAVA를 사용하여 프로그램을 사용하였습니다. 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다. public class Main{
tussle.tistory.com
https://tussle.tistory.com/279?category=972975
[백준] 단계별로 풀어보기(단계:17,정수론 및 조합론,JAVA)11050번, 이항 계수 1
문제 링크 11050번: 이항 계수 1 www.acmicpc.net 주의사항 JAVA를 사용하여 프로그램을 사용하였습니다. 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다. public class Ma
tussle.tistory.com
https://tussle.tistory.com/282?category=972975
[백준] 단계별로 풀어보기(단계:17,정수론 및 조합론,JAVA)11051번, 이항 계수 2
문제 링크 11051번: 이항 계수 2 www.acmicpc.net 주의사항 JAVA를 사용하여 프로그램을 사용하였습니다. 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다. public class Ma
tussle.tistory.com
추가
알고리즘 문제를 풀어보던 중 이항계수의 N과 K의 값이 매우 큰 수가 들어와서
자료형을 넘어버려서 나머지를 구하라는 문제를 만나서 위에 파스칼 트리를 이용한 알고리즘도 실패하였습니다.
그에 맞게 분할 정복과 페르마 소정리를 이용한 내용을 링크로 올려두겠습니다.
[백준] 단계별로 풀어보기(단계:20,분할 정복,JAVA)11401번, 이항 계수 3
문제 링크 11401번: 이항 계수 3 www.acmicpc.net 주의사항 JAVA를 사용하여 프로그램을 사용하였습니다. 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다. public class Ma
tussle.tistory.com
'JAVA' 카테고리의 다른 글
| Spring Cache를 파헤쳐 보자!(WebMvc, WebFlux) (0) | 2023.12.13 |
|---|---|
| [JAVA] Character형 숫자, 알파벳인지 확인하기 Character.isDigit/Character.isAlphabetic (0) | 2023.02.19 |
| [JAVA] 배열 및 객체 정렬하는 방법 Arrays.sort, Collections.sort (0) | 2022.01.13 |
| [JAVA] 숫자 큰값/작은값 비교하기 Math.max/Math.min (0) | 2022.01.04 |
| [JAVA] 숫자 제곱근(루트) 구하는 방법 Math.sqrt() (0) | 2022.01.02 |

댓글