문제 링크
11066번: 파일 합치기
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
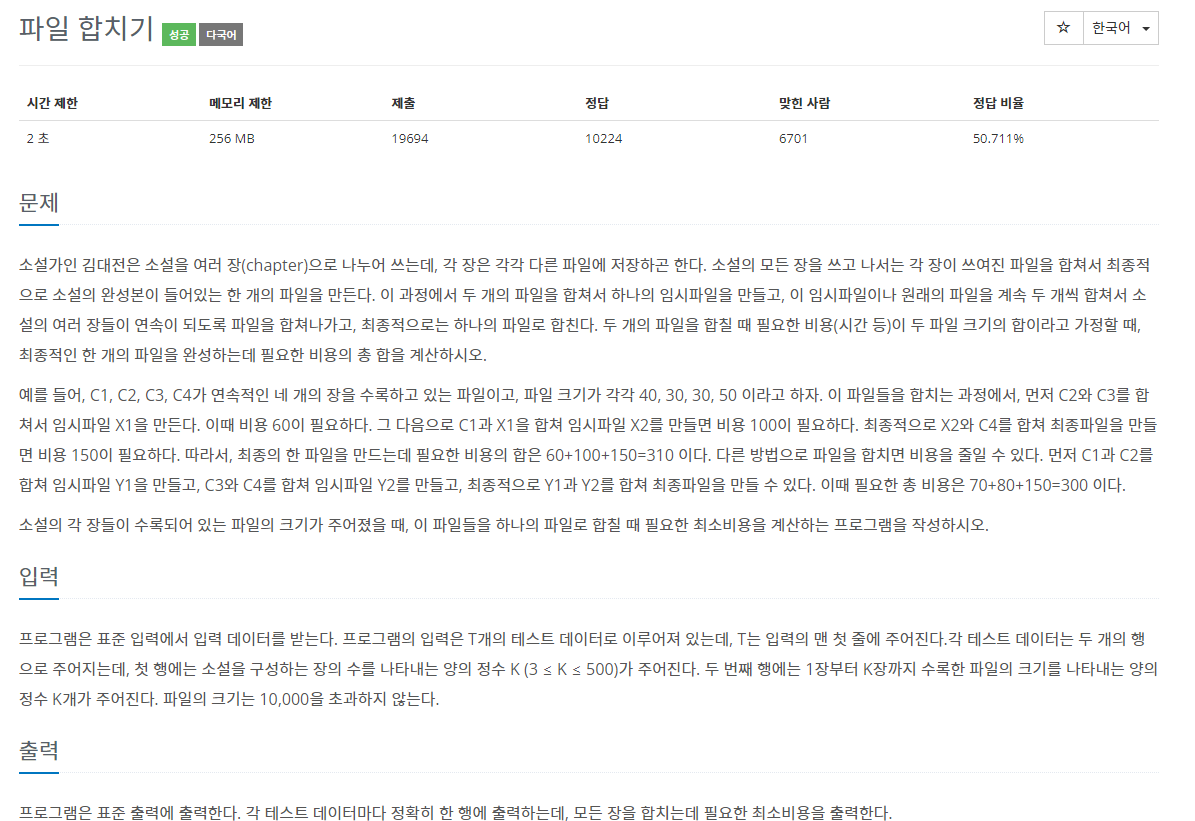
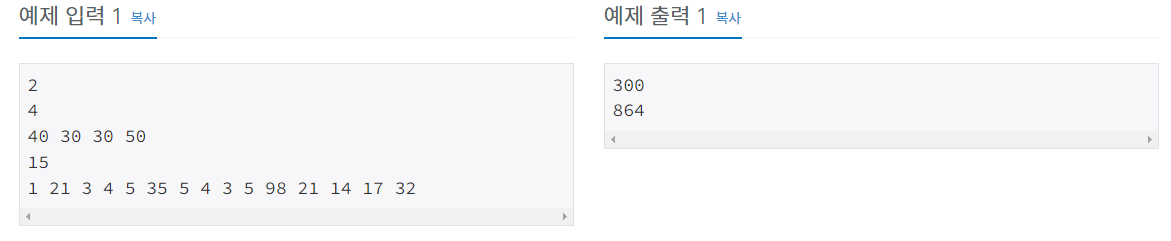
접근 방법
동적계획법이란 위 문제와 같이 동일한 연산을 계속 반복하여 비효율적으로 코드가 실행되어 그것을 향상시키기 위하여반복되는 연산의 결과를 따로 저장하여 적재적소에 코드가 더 효율적으로 만드는 방법입니다.
문제의 정답 비율이 50%이지만 저는 쉽게 해결하지 못하였습니다.
먼저 저는 어떤 규칙이 존재할 것 같다고 생각하여 여러가지 방법을 시도해보았지만 찾지 못하였습니다.
검색을 통해 찾아본 바 메모이제이션 DP[j][i]일 때 j번째 챕터부터 i번째 챕터를 합쳤을 때 최소값을 저장하는 것을 반복으로 DP를 모두 저장하였을 때 DP[1][K]의 값을 구하는 것으로 챕터들을 합쳤을 때 최소 비용을 구할 수 있습니다.
예를 들어 A1, A2 ,A3, A4 존재시
DP[1][3]은 A1, A2, A3를 합쳤을 때 최소비용
DP[2][4]는 A2, A3, A4를 합쳤을 때 최소비용으로 표현할 수 있습니다.
최소비용을 구할 시
A1, A2, A3가 존재하면 챕터를 합칠 수 있는 경우의 수는
1. (A1, A2), A3 : A1과 A2를 먼저 합친 후 A3와 합치기
2. A1, (A2, A3) : A2와 A3를 먼저 합친 후 A1과 합치기
※ 문제에서 인접한 챕터끼리만 합칠 수 있다는 조건이 존재하기에 A1과 A3은 합칠 수 없습니다.
식으로 살펴보면
1번에서 (A1, A2)는 DP[1][2]로 표현하고 A3은 DP[3][3]으로 표현한 뒤
A1, A2, A3는 무조건 한 번씩 합쳐지기 때문에1~3까지의 비용값을 모두 더해주어야 합니다.
※sum[]은 해당 인덱스까지의 비용 합입니다. (예제입력 1에서 sum[2] = 40 + 30 = 70이 됩니다.)
DP[1][2] + DP[3][3] + sum[3] - sum[0]이 나옵니다.
2번도 1번과 동일하게 표현하면
DP[1][1] + DP[2][3] + sum[3] - sum[0]이 나옵니다.
다른 예시로 A2, A3, A4가 합쳐진다면(범위 2~4)
(A2, A3), A4 : DP[2][3] + DP[4][4] + sum[4] - sum[1]
A2 , (A3, A4) : DP[2][2] + DP[3][4] + sum[4] - sum[1]
※sum[4] - sum[1]인 이유는 2~4범위로 A2, A3, A4의 비용의 합만 필요하기 때문입니다.
이렇게 보면 공식이 발견됩니다.
i : 목적지, j : 출발지, s : 합치는 구역(j ≤ s < i), 범위 : j~i
DP[j][i] = DP[i][s] + DP[s+1][j] + sum[i] - sum[j-1]에서 s의 범위 중 최소값으로 표현할 수 있습니다.
더 간소화하면 sum[i] - sum[j-1]은 s가 범위 내 무슨 값이든 동일하기 때문에
DP[j][i] = DP[i][s] + DP[s+1][j] 가 가장 작은 값에서 sum[i] - sum[j-1]을 해주면 됩니다.
이제는 어떤 순서로 DP를 구해야하는지 고민을 해보았습니다.
구해야하는 DP값은 DP[1][K]의 값으로써 목적지를 2부터 시작하면 됩니다.
즉 DP[1][2]->DP[2][3] -> DP[1][3] -> DP[3][4] -> DP[2][4] -> DP[1][4] .....이렇게 진행되게 하였습니다.
문제를 해결한 알고리즘의 과정입니다.
1. DP[i][j]의 값을 Integer.MAX_VALUE로 초기화해줍니다.
2. DP[1][2]을 시작으로 DP[1][K]까지 구해줍니다.
3. DP[1][K]을 결과로 출력합니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- StringTokenizer을 이용하여 비용값들을 받고 sum[] 배열을 초기화해주었습니다.
- 파일 최소 비용 구하는 fileMerge 함수를 만들었습니다.
- BufferedWriter에 DP[1][K]의 값을을 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- fileMerge는 3중 반복문을 통해서 DP[1][2]부터 DP[1][K]까지의 최소비용 값을 구하였습니다.
- fileMerge는 위에 설명한 알고리즘 대로 DP를 이용해 최소값을 구한 뒤 sum[]을 이용하여 범위에 속하는 비용들을 더해주었습니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
public static int[] sum = new int[501]; //파일 비용 합 저장 배열
public static int[][] DP = new int[501][501]; //j->i 합치는 최소 비용 저장 배열
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
//-----입력값 저장 및 배열 초기화--------
int T = Integer.parseInt(br.readLine());
StringTokenizer st;
for(int i=0;i<T;i++) {
int K = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine()," ");
for(int j=1;j<=K;j++) {
sum[j] = sum[j-1] + Integer.parseInt(st.nextToken());
}
fileMerge(K); //함수 실행
bw.write(DP[1][K] + "\n"); //결과 저장
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//----------파일 최소 비용 구하는 함수---------
public static void fileMerge(int K) {
for(int i=2;i<=K;i++) { //목적지 2부터 시작
for(int j=i-1;j>=1;j--) { //출발지 i-1부터 시작
DP[j][i] = Integer.MAX_VALUE;
for(int s=j;s<i;s++) { //중간지점 j부터 시작
DP[j][i] = Math.min(DP[j][i], DP[j][s] + DP[s+1][i]); //최소값 정하기
}
DP[j][i] += sum[i] - sum[j-1]; //비용합 더하기
}
}
}
}'백준' 카테고리의 다른 글
| [백준] 단계별로 풀어보기(단계:23,동적 계획법 2,JAVA)11049번, 행렬 곱셈 순서 (0) | 2022.03.12 |
|---|---|
| [백준] code.plus(브루트포스,JAVA)15655번, N과 M(6) (0) | 2022.03.12 |
| [백준] code.plus(브루트포스,JAVA)15654번, N과 M(5) (0) | 2022.03.10 |
| [백준] 단계별로 풀어보기(단계:22,우선순위 큐,JAVA)1655번, 가운데를 말해요 (0) | 2022.03.09 |
| [백준] code.plus(브루트포스,JAVA)9095번, 1, 2, 3 더하기 (0) | 2022.03.09 |




댓글