[백준] 단계별로 풀어보기(단계:23,동적 계획법 2,JAVA)10942번, 팰린드롬?

문제 링크

10942번: 팰린드롬?

---

주의사항

• JAVA를 사용하여 프로그램을 사용하였습니다.
• 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.

public class Main{ 	
	public static void main(String[] args){
    }
}

---

문제 설명

---

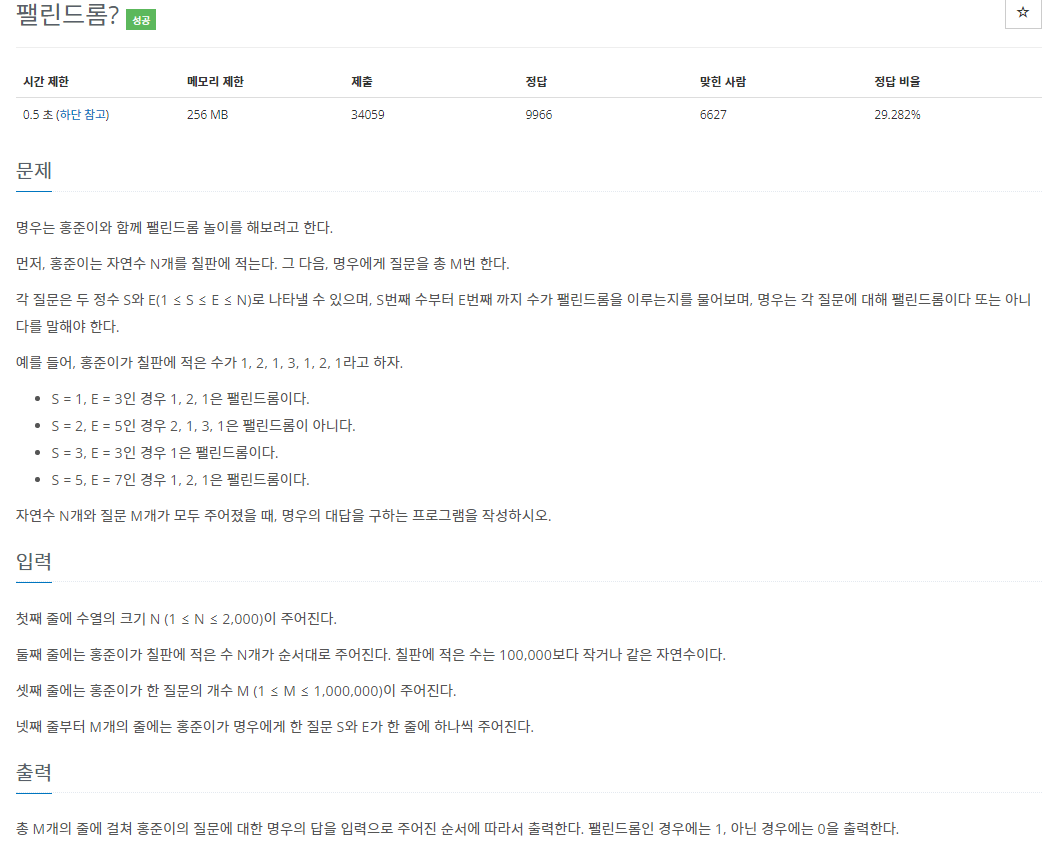
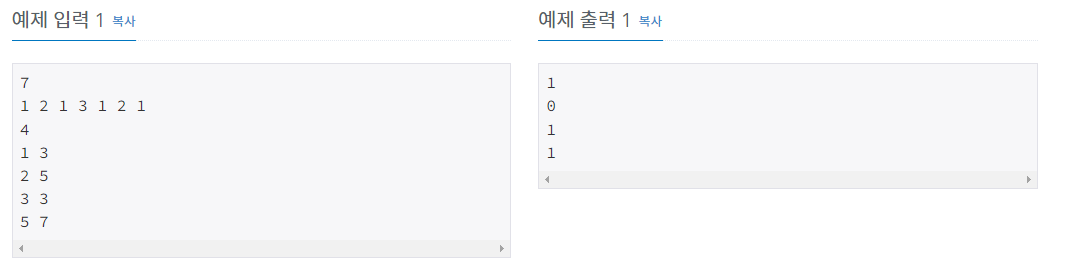
접근 방법

동적계획법이란 위 문제와 같이 동일한 연산을 계속 반복하여 비효율적으로 코드가 실행되어 그것을 향상시키기 위하여반복되는 연산의 결과를 따로 저장하여 적재적소에 코드가 더 효율적으로 만드는 방법입니다.

이 문제에서 설명하는 팰린드롬이라는 규칙을 알지 못하여 검색을 해보았으며 아래 링크를 남깁니다.

회문 - 위키백과, 우리 모두의 백과사전

팰린드롬는 회문으로 거꾸로 읽어도 제대로 읽은 것과 같은 문장을 설명하는 것입니다.예를 들어

 

1 2 3 2 1은 순서대로 읽거나 거꾸로 읽어도 동일하게 읽어서 팰린드롬이 맞습니다.

 

1 2 4 3 1은 순서대로 읽으면 1 2 4 3 1 거꾸로 읽으면 1 3 4 2 1로 서로 다르기 때문에 팰린드롬이 아닙니다.

 

메모이제이션 DP[i][j]일 때 값은 i부터 j까지 범위가 팰린드롬인지 확인하는 값을 저장하였습니다.

1 : 팰린드롬이 맞다.

0 : 팰린드롬이 아니다.

-1 : 아직 탐색하지 않았습니다.

 

예제입력1에서 예를 들면

 

DP[1][3] = 1이면 팰린드롭이 맞다.

 

DP[2][5] = 0이면 팰린드롭이 아니다.

 

이제 팰린드롭을 확인하는 것에 대하여 말씀드리겠습니다.

 

문장이 거꾸로도 읽으려면 범위의 시작과 끝이 동일한 숫자를 가지고 있어야 하며

 

범위가 점점 감소할 때에도 감소한 범위에 시작과 끝은 동일한 숫자를 가져야 합니다.

 

범위는 S나 E가 중간값이 될 때까지 감소를 진행해야 합니다.

 

해당 범위에 S = 1, E = 5의 범위로 팰린드롭이 맞는지 확인하는 것은

1(S)

2

3

2

1(E)

1. 범위의 S값과 E값 비교 : 1(S) == 1(E)

현재까지 범위는 팰린드롭이 맞습니다.

2. 범위를 감소한다.

1

2(S)

3

2(E)

1

3. 범위의 S값과 E값 비교 : 2(S) == 2(E)

현재까지 범위는 팰린드롭이 맞습니다.

4. 범위를 감소한다.

1

2

3(S,E)

2

1

5. 범위의 S값과 E값 비교 : 3(S)==3(E)

범위 감소는 중간값까지 진행하기 때문에 더 이상 범위 감소는 진행하지 않으며

범위를 감소하면서 탐색해보았을 때 범위의 S값과 E값이 같았기 때문에 팰린드롭이 맞습니다.

결과적으로

DP[3][3] = 1

DP[2][4] = 1

DP[1][5] = 1

범위 S=1,  E=5는 팰린드롭이 맞다는 것을 표현할 수 있습니다.

수가 짝수개일 때에도 적용이 가능합니다. S = 1, E = 4 범위일 때

1(S)

2

2

1(E)

1. 범위의 S값과 E값 비교 : 1(S) == 1(E)

현재까지 범위는 팰린드롭이 맞습니다.

2. 범위를 감소한다.

1

2(S)

2(E)

1

3. 범위의 S값과 E값 비교 : 2(S)==2(E)

범위 감소는 중간값까지 진행하기 때문에 더 이상 범위 감소는 진행하지 않으며

범위를 감소하면서 탐색해보았을 때 범위의 S값과 E값이 같았기 때문에 팰린드롭이 맞습니다.

결과적으로

DP[2][3] = 1

DP[1][4] = 1

범위 S=1,  E=4는 팰린드롭이 맞다는 것을 표현할 수 있습니다.

문제를 해결한 알고리즘의 과정입니다.

1. DP[][]의 값을 -1로 초기화해줍니다.

2. DP[0][0]을 기준으로 재귀를 통해 팰린드롭이 맞는지 확인하였습니다.

3. DP가 -1이 아니면 해당 DP값을 반환하고 아니면 탐색을 진행합니다.

4. DP[S][E]을 결과로 출력합니다.

 

 

• BufferedReader를 사용하여 입력 값을 받았습니다.
• StringTokenizer을 이용하여 비용값들을 받고 num 배열을 초기화해주었습니다.
• 팰린드롭 맞는지 확인하는 palindrome 함수를 만들었습니다.
• BufferedWriter에 DP[S][E]의 값을 저장하였습니다.
• BufferedWriter에 저장된 결과값을 출력하였습니다.

• palindrome은 재귀를 통해 DP[S][E]에서 범위를 감소하면서 탐색하였습니다. 
• palindrome은 위에 설명한 알고리즘 대로 DP와 num를 이용하여 팰린드롭이 맞는지를 구하였습니다.

 

결과 코드

import java.io.*;
import java.util.*;
public class Main{
	public static int[] num;		//숫자 저장 배열
	public static int[][] DP;		//팰린드롭 확인 배열
    public static void main(String[] args) throws IOException{
    	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        //입력값 처리하는 BufferedReader
    	BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        //결과값 출력하는 BufferedWriter
        //----------입력값 저장 및 배열 초기화--------
    	int N = Integer.parseInt(br.readLine());
    	num = new int[N+1];
    	DP = new int[N+1][N+1];
    	StringTokenizer st = new StringTokenizer(br.readLine()," ");
    	for(int i=1;i<=N;i++) {
    		Arrays.fill(DP[i], -1);		//DP -1로 초기화
    		num[i] = Integer.parseInt(st.nextToken());
    	}
    	int M = Integer.parseInt(br.readLine());
    	for(int i=0;i<M;i++) {
    		st = new StringTokenizer(br.readLine()," ");
    		int S = Integer.parseInt(st.nextToken());
    		int E = Integer.parseInt(st.nextToken());
    		int median = (S + E)/2;		//중간값
    		palindrome(S,E,median);		//함수 실행
    		bw.write(DP[S][E] + "\n");	//DP[S][E] 결과 BufferedWriter 저장
    	}
    	bw.flush();		//결과 저장
    	bw.close();
    	br.close();
    }
    //--------팰린드롭 확인 함수-------
    public static int palindrome(int curS, int curE, int median) {
    	if(curS==median || curE==median) {		//중간값까지 범위 감소하였을 때
    		if(num[curS]==num[curE]) {
    			DP[curS][curE] = 1;		//팰린드롭 맞음
    		}else
    			DP[curS][curE] = 0;		//팰린드롭 아님
    		return DP[curS][curE];
    	}
    	if(DP[curS][curE]!=-1)		//DP[][] 탐색 했을 때
    		return DP[curS][curE];
    	
    	if(num[curS] == num[curE]) {	//해당 범위 팰린드롭 맞을 때
        	// 범위 감소 후 탐색
    		DP[curS][curE] = palindrome(curS+1, curE-1, median);
    	}else
    		DP[curS][curE] = 0;		//팰린드롭 아님
    	
    	return DP[curS][curE];		//결과 반환
    	
    }
}