주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
최단경로는 시작 정점에서 목표 정점까지 최소의 비용으로 갈 수 있는 경로를 구하는 것입니다.
최단 경로를 구하는 알고리즘은 대표적으로 3개가 존재합니다.
1. 다익스트라 알고리즘
2. 벨만-포드 알고리즘
3. 플로이드 워셜 알고리즘
3가지 알고리즘은 문제를 해결할 때 사용하는 알고리즘만 설명하도록 하겠습니다.
다익스트라 알고리즘이란?

1. 출발 정점에서 인접한 정점으로 이동합니다.
2. 인접한 정점에서 가장 적은 가중치(거리)의 정점을 먼저 탐색합니다.
3. 이동을 할 때마다 이동한 거리가 현재 저장된 거리보다 작으면 변경합니다.
4. 위 과정을 반복이 끝나면 출발 정점에서 각 정점에 도착하는 최소 거리을 구할 수 있습니다.
글로는 잘 설명하지 못한 것 같아서 아래에 예제 문제를 풀면서 어떻게 진행되는지 자세히 보여드리겠습니다.
더 자세한 내용은 아래 링크를 통해 확인해주시기 바랍니다.
데이크스트라 알고리즘 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서, 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.
ko.wikipedia.org
이 문제에 핵심은
1. 입력값으로 주는 내용은 모두 그래프의 내용입니다.
2. 시작점에서 도착점까지의 최소 거리를 출력해야 합니다.
3. 시작점에서 시작점으로 갈 때에는 0, 시작점에서 도착점까지 도착못하면 INF를 출력합니다.
4. 여러개의 간선이 존재할 수 있다 = 방향이 정해진 간선이다.
저는 BFS(너비우선탐색)와 다익스트라 알고리즘을 사용하여 해결하였습니다.
그래프에 대한 내용을 정의하기 위해 ArrayList<ArrayList<Integer>>의 형태로 리스트를 만들어주었습니다.
위와 같이 정의하여 데이터를 저장하면 각 정점이 어떤 정점으로 이동하는지 간단하게 저장할 수 있습니다.
예를 들어
1 -> 4
1 -> 3
2 -> 5
3 -> 4
ArrayList<ArrayList<Integer>>의 저장되는 모습은 리스트 안에 리스트가 포함되는 형식으로 저장됩니다.
| 정점 | ||
| 1 | 3 | 4 |
| 2 | 5 | |
| 3 | 1 | 4 |
| 4 | 1 | 4 |
| 5 | 2 |
그래프의 값을 리스트에 저장하였다면 각 정점을 기준으로 BFS탐색으로 다익스트라 알고리즘을 구현하였습니다..
예제 입력1에서 첫 번째 테스트케이스의 그래프를 표로 확인하며 보여드리겠습니다.
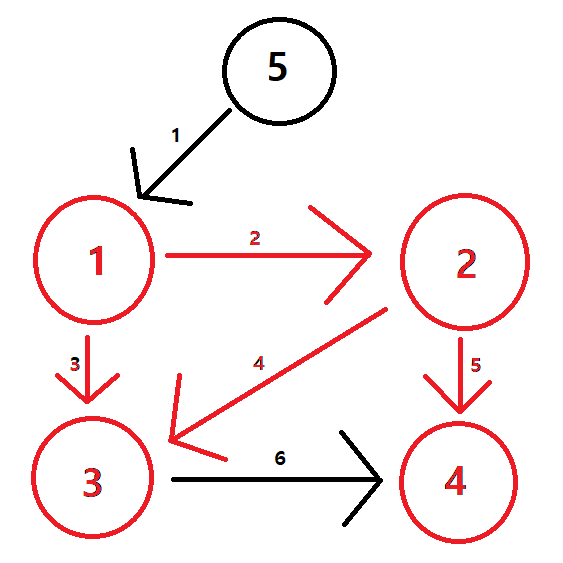
아래는 예제로 주어진 그래프입니다.

그래프의 내용이 저장된 ArrayList<ArrayList<>>의 해당하는 표
| 정점 | ||
| 1 | 2(거리 : 2) | 3(거리 : 3) |
| 2 | 3(거리 : 4) | 4(거리 : 5) |
| 3 | 4(거리 : 6) | |
| 4 | ||
| 5 | 1(거리 : 1) |
출발 정점1에서 각 지점의 최소 거리을 정리한 표(자신 거리는 = 0, 아직 가보지 않은 곳은 INF(무한대)로 표현)
| 1 | 2 | 3 | 4 | 5 |
| 0 | INF | INF | INF | INF |
1. 출발 정점 1에서 인접한 정점으로 이동합니다.
정점 2로 이동합니다.

| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | INF | INF | INF |
원래 표의 정점 2의 거리는 INF로써
2 < INF이므로 INF가 2로 변경되었습니다.
정점 3으로 이동합니다.

| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | INF | INF |
원래 표의 정점 3의 거리는 INF로써
3 < INF이므로 INF가 3으로 변경되었습니다.
2. 간선에 거리가 적었던 정점 2에서 인접한 정점을 탐색합니다.
정점 3으로 이동합니다.

| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | INF | INF |
현재 정점의 거리 : 2, 간선의 거리 : 4 = 2 + 4 = 6
원래 표의 정점 3의 거리는 3으로
6 > 3이므로 변경되지 않았습니다.
정점 4으로 이동합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | 7 | INF |
현재 정점의 거리 : 2, 간선의 거리 : 5 = 2 + 5 = 7
원래 표의 정점 4의 거리가 INF으로
7 < INF이므로 INF가 7으로 변경되었습니다.
3. 다음 정점 1의 인접하여 거리가 적은 정점 3을 탐색합니다.
정점 4로 이동합니다.

| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | 7 | INF |
현재 정점의 거리 : 3, 간선의 거리 : 6 = 3 + 6 = 9
원래 표의 정점 3의 거리는 3으로
9 > 7이므로 변경되지 않았습니다.
4. 더 이상 탐색할 수 있는 간선이 존재하지 않기 때문에 탐색을 종료합니다!
현재 최소 거리가 저장된 표를 순서대로 결과로 출력합니다.
| 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | 7 | INF |
문제를 해결한 알고리즘의 과정입니다.
1. 그래프에 대한 정보를 ArrayList<ArrayList<Integer>>에 저장합니다.
2. BFS(너비 우선 탐색)을 이용하여 출발 정점에 간선을 탐색합니다.
3. 다음 정점은 거리가 적은 정점을 먼저 탐색합니다.
4. 모든 탐색이 종료되면 최소 거리 배열에 저장된 값을 출력합니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- StringTokenizer를 통해 그래프에 대한 정보를 저장하였습니다.
- 그래프에 사용할 point(정점), cost(거리)를 저장하는 node 생성자를 만들었습니다.
- 그래프에 내용 저장할 ArrayList<ArrayList<Integer>> graph를 만들었습니다.
- BFS로 최단 경로(다익스트라)를 구하는 shortestPath 함수를 만들었습니다.
- BufferedWriter에 최소 거리 배열에 저장된 값들을 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- shortestPath은 distance[], graph와 PriorityQueue를 통해 인접한 정점을 탐색하였습니다.
- shortestPath는 다익스트라 알고리즘과 BFS를 구조를 이용하여 작성하였습니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
//정점과 비용을 저장하는 생성자
public static class node{
int point, cost;
public node(int point, int cost) {
this.point = point;
this.cost = cost;
}
public int getPoint() {
return point;
}
public int getCost() {
return cost;
}
}
public static int V,E, start;
public static int[] distance; //최소 거리 저장 배열
public static ArrayList<ArrayList<node>> graph = new ArrayList<>(); //그래프 값
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
//-------입력값 저장, 배열 초기화, 리스트 초기화---------
StringTokenizer st = new StringTokenizer(br.readLine()," ");
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
start = Integer.parseInt(br.readLine());
distance = new int[V+1];
for(int i=0;i<V+1;i++) {
graph.add(new ArrayList<>());
}
for(int i=0;i<E;i++) {
st = new StringTokenizer(br.readLine()," ");
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
graph.get(u).add(new node(v,w));
}
for(int i=1;i<=V;i++)
distance[i] = Integer.MAX_VALUE;
distance[start] = 0;
shortestPath(); //BFS를 통한 최단 경로(다익스트라) 함수 실행
for(int i = 1;i<=V;i++) {
if(distance[i] == Integer.MAX_VALUE) //도달하지 못하는 정점일 때
bw.write("INF\n");
else
bw.write(distance[i] + "\n"); //도달한 정점의 최소 거리
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//-------BFS를 통해 최단 경로(다익스트라)을 구하는 함수---------
public static void shortestPath() {
/*
우선순위 큐를 사용해서 현재 정점들에서 거리가 가장 적은 정점을
바로 poll()을 할 수 있도록 거리가 작은 순으로 Queue에 저장되도록
Comparator를 설정해주었습니다.
*/
PriorityQueue<node> queue = new PriorityQueue<node>(new Comparator<node>() {
@Override
public int compare(node o1, node o2) {
return o1.cost-o2.cost;
}
});
queue.add(new node(start, 0)); //출발 정점 큐에 저장
while(!queue.isEmpty()) {
node temp = queue.poll();
/*
정점에 도착했을 때 최소 거리보다 크면
해당 정점에 간선 어디를 가도 최소 거리가 되지 않기 때문에
해당 탐색을 그대로 넘어갔습니다.
*/
if(distance[temp.point] < temp.cost)
continue;
//최소 거리보다 작을 때
for(int i=0;i<graph.get(temp.point).size();i++) {
node next = graph.get(temp.point).get(i);
if(distance[next.point] > distance[temp.point] + next.cost) {
distance[next.point] = distance[temp.point] + next.cost;
queue.add(new node(next.point,distance[next.point]));
}
}
}
return;
}
}'백준' 카테고리의 다른 글
| [백준] 단계별로 풀어보기(단계:25, 최단 경로,JAVA)1504번, 특정한 최단 경로 (0) | 2022.04.03 |
|---|---|
| [백준] code.plus(다이나믹 프로그램 part 1,JAVA)11727번, 2×n 타일링 2 (0) | 2022.04.03 |
| [백준] code.plus(다이나믹 프로그램 part 1,JAVA)11726번, 2×n 타일링 (0) | 2022.04.01 |
| [백준] 단계별로 풀어보기(단계:24, DFS와BFS,JAVA)1707번, 이분 그래프 (0) | 2022.04.01 |
| [백준] code.plus(브루트포스-비트마스크,JAVA)14391번, 종이 조각 (0) | 2022.04.01 |




댓글