주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
최단경로는 시작 정점에서 목표 정점까지 최소의 비용으로 갈 수 있는 경로를 구하는 것입니다.
최단 경로를 구하는 알고리즘은 대표적으로 3개가 존재합니다.
1. 다익스트라 알고리즘
2. 벨만-포드 알고리즘
3. 플로이드 워셜 알고리즘
3가지 알고리즘은 문제를 해결할 때 사용하는 알고리즘만 설명하도록 하겠습니다.
다익스트라 알고리즘이란?

1. 출발 정점에서 인접한 정점으로 이동합니다.
2. 인접한 정점에서 가장 적은 가중치(거리)의 정점을 먼저 탐색합니다.
3. 이동을 할 때마다 이동한 거리가 현재 저장된 거리보다 작으면 변경합니다.
4. 위 과정을 반복이 끝나면 출발 정점에서 각 정점에 도착하는 최소 거리을 구할 수 있습니다.
글로는 잘 설명하지 못한 것 같아서 아래에 예제 문제를 풀면서 어떻게 진행되는지 자세히 보여드리겠습니다.
더 자세한 내용은 아래 링크를 통해 확인해주시기 바랍니다.
데이크스트라 알고리즘 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서, 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.
ko.wikipedia.org
이 문제에 핵심은
1. 입력값으로 주는 내용은 모두 그래프의 내용입니다.
2. 방향성이 있는 간선이다.
3. 동일한 정점의 방향으로 비용과 기간만 다른 경우가 존재한다.
4. 출발 정점에서 목적 정점에 도착하지 못한다면 Poor KCM을 출력합니다.
문제를 접근할 때 동일한 방향의 비용과 기간만 다른 경우가 존재하지 않을 것이라고 생각하고 진행하였습니다.
코드를 작성한 뒤 제출해보니 "틀렸습니다."가 나왔고 다른 반례가 존재하는지 질문 게시판을 통해 확인하였을 때
핵심3번처럼 동일한 정점의 방향으로 비용과 기간만 다른 경우가 존재한다는 것을 알게되어 수정하였습니다.
저는 BFS를 통해 다익스트라 알고리즘을 구현하여 해결하였습니다.
그래프에 대한 내용을 정의하기 위해 ArrayList<ArrayList<Integer>>의 형태로 리스트를 만들어주었습니다.
위와 같이 정의하여 데이터를 저장하면 각 정점이 어떤 정점으로 이동하는지 간단하게 저장할 수 있습니다.
예를 들어
1 -> 4
1 -> 3
2 -> 5
3 -> 4
ArrayList<ArrayList<Integer>>의 저장되는 모습은 리스트 안에 리스트가 포함되는 형식으로 저장됩니다.
| 정점 | ||
| 1 | 3 | 4 |
| 2 | 5 | |
| 3 | 1 | 4 |
| 4 | 1 | 4 |
| 5 | 2 |
그래프의 값을 리스트에 저장하였다면 각 정점을 기준으로 BFS탐색으로 다익스트라 알고리즘을 구현하였습니다.
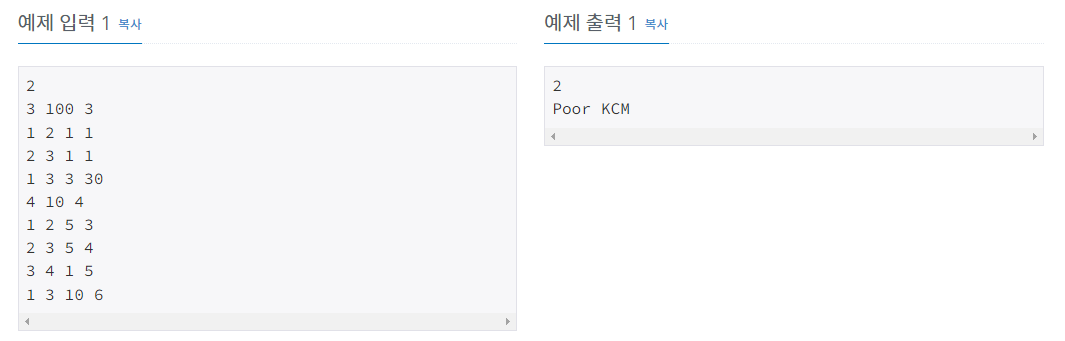
예제 입력1의 첫 번째 케이스에 대하여 살펴보겠습니다.
아래는 예제로 주어진 그래프입니다.

그래프의 내용이 저장된 ArrayList<ArrayList<>>의 해당하는 표
| 정점 | ||
| 1 | 2(비용 : 1, 기간 : 1) | 3(비용 : 3, 기간 : 30) |
| 2 | 3(비용 : 1, 기간 : 1) | |
| 3 |
출발 정점1에서 각 지점의 최소 거리을 정리한 표(자신 거리는 = 0, 아직 가보지 않은 곳은 INF(무한대)로 표현)는
동일한 방향에 비용과 소요시간만 다른 비행 티켓이 존재하기 때문에 최소 거리를 저장하는 표를 비용별로 저장해야 합니다.
distance[정점][비용]으로 표현할 수 있습니다.
출발 정점은 distance[1][0] = 0으로 초기화하고 나머지 값들은 INF로 초기화를 해줍니다.
1. 출발 정점 1에서 인접한 정점으로 이동합니다.
정점 2으로 이동합니다.

정점 2까지 가는 비용 = 1, 소요시간 = 1로distnace[2][1] = 1이 저장됩니다.
정점 3으로 이동합니다.

정점 3까지 가는 비용 = 3, 소요시간 = 30distance[3][3] = 30
2. 간선에 거리가 적었던 정점 2에서 인접한 정점을 탐색합니다.
정점 3으로 이동합니다.

현재 정점의 비용 : 1, 소요시간 : 1
간선의 비용 : 1, 소요시간 : 1
비용 = 1 + 1 = 2
소요시간 = 1 + 1 = 2
distance[3][2] = 2
4. 더 이상 탐색할 수 있는 간선이 존재하지 않기 때문에 탐색을 종료합니다!
이제 결과를 출력할 때
distance[n][0~최대비용] 중 가장 소요시간이 짧은 값을 출력하면 됩니다.만약 distance[n][0~최대비용]의 모든 값이 INF이면 도착하지 못한다고 판단하여 Poor KCM을 출력합니다
예제입력1 첫 번째 테스트케이스에서는
distance[3][0~최대비용] 값 중에 존재하는 2와 30 중 작은 2가 결과로 출력합니다.
문제를 해결한 알고리즘의 과정입니다.
1. 그래프에 대한 정보를 ArrayList<ArrayList<Integer>>에 저장합니다.
2. BFS(너비 우선 탐색)을 이용하여 출발 정점에 간선을 탐색합니다.
3. 다음 정점은 거리가 적은 정점을 먼저 탐색합니다.
4. 최소거리를 저장할 때 비용에 따라 저장하도록 하였습니다.
5. 모든 탐색이 종료되면 distance[n][0~최대비용]의 값 중 최소 값을 결과로 출력하였습니다.
6. distance[n][0~최대비용]의 값이 모두 INF이면 Poor KCM을 출력하도록 하였습니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- StringTokenizer를 통해 그래프에 대한 정보 분리하였습니다.
- BFS으로 최단 경로(다익스트라 알고리즘)를 구하는 shortestPath 함수를 만들었습니다.
- 출발 정점에서 도착 지점까지 비용별 최단 경로를 구하였습니다.
- BufferedWriter에 distance[N][0~최대비용] 중 최소 기간의 값을 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- shortestPath은 distance[정점][비용]을 통해 각 비용별 최단 경로를 구하였습니다.
- shortestPath는 다익스트라 알고리즘과 BFS을 이용하여 작성하였습니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
//항공 관련 생성자
public static class airport implements Comparable<airport> {
int point, cost, perid;
public airport(int point, int cost, int perid) {
this.point = point; //도착 지점
this.cost = cost; //비용
this.perid = perid; //소요 기간
}
@Override
public int compareTo(airport o) {
return this.perid - o.perid;
}
public int getPoint() {
return point;
}
public int getCost() {
return cost;
}
public int getPerid() {
return perid;
}
}
public static ArrayList<ArrayList<airport>> graph = new ArrayList<>(); //그래프 값
public static int[][] distance; //최단 거리 저장 배열 distance[정점][비용]
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
//-----입력값 저장 및 그래프 초기화----
StringTokenizer st;
int T = Integer.parseInt(br.readLine());
for(int i=0;i<T;i++) {
st = new StringTokenizer(br.readLine()," ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
for(int j=0;j<=N;j++)
graph.add(new ArrayList<>());
for(int j=0;j<K;j++) {
st = new StringTokenizer(br.readLine()," ");
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
graph.get(u).add(new airport(v, c, d)); //그래프 값 저장
}
for(int j=0;j<N;j++){
Collections.sort(graph.get(j));
}
distance = new int[N+1][M+1]; //최소 거리 저장 배열 초기화
shortestPath(1, N, M); //다익스트라 알고리즘 실행
int result = Integer.MAX_VALUE/2;
for(int j=0;j<=M;j++) { //distance[N][0~최대비용] 중 최소경로 값 구하기
result = Math.min(result, distance[N][j]);
}
if(result==Integer.MAX_VALUE/2) //모든 값이 INF일 때
bw.write("Poor KCM\n");
else //최소 경로 값 BufferedWriter 저장
bw.write(result + "\n");
graph.clear(); //그래프 초기화
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//BFS를 통한 다익스트라 알고리즘 수행 함수
public static void shortestPath(int start, int end, int maxCost) {
PriorityQueue<airport> queue = new PriorityQueue<>();
//distance[][] INF로 초기화
//저는 INF = Integer.MAX_VALUE / 2로 설정하였습니다.
for(int i=1;i<=end;i++)
Arrays.fill(distance[i], Integer.MAX_VALUE/2);
//출발 정점 0으로 초기화
distance[start][0] = 0;
queue.add(new airport(start, 0, 0));
while(!queue.isEmpty()) {
airport temp = queue.poll();
int point = temp.getPoint();
int cost = temp.getCost();
int perid = temp.getPerid();
/*
정점에 도착했을 때 최소 거리보다 크면
해당 정점에 간선 어디를 가도 최소 거리가 되지 않기 때문에
해당 탐색을 그대로 넘어갔습니다.
*/
if(distance[point][cost] < perid)
continue;
for(airport value : graph.get(point)) {
int nextCost = cost + value.getCost();
int nextPerid = perid + value.getPerid();
if(maxCost >= nextCost) { //최대 비용 넘지 않았을 때
if(distance[value.getPoint()][nextCost] > nextPerid) {
distance[value.getPoint()][nextCost] = nextPerid;
queue.add(new airport(value.getPoint(), nextCost, nextPerid));
}
}
}
}
}
}'백준' 카테고리의 다른 글
| [백준] 단계별로 풀어보기(단계:25, 최단 경로,JAVA)1956번, 운동 (0) | 2022.04.08 |
|---|---|
| [백준] code.plus(다이나믹 프로그램 part 1,JAVA)14002번, 가장 긴 증가하는 부분 수열 4 (0) | 2022.04.08 |
| [백준] code.plus(다이나믹 프로그램 part 1,JAVA)2193번, 이친수 (0) | 2022.04.07 |
| [백준] 단계별로 풀어보기(단계:25, 최단 경로,JAVA)11404번, 플로이드 (0) | 2022.04.07 |
| [백준] code.plus(다이나믹 프로그램 part 1,JAVA)15990번, 1, 2, 3 더하기 5 (0) | 2022.04.06 |




댓글