문제 링크
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
다이나믹 프로그램
모든 연산을 수행하면 똑같은 연산을 중복되게 수행하게 되는데 다이나믹 프로그램은 연산한 내용을 따로 저장하여 효율적으로 작성한 프로그램입니다.
더 자세한 내용은 링크를 남겨두겠습니다.
동적 계획법 - 위키백과, 우리 모두의 백과사전
수학과 컴퓨터 과학, 그리고 경제학에서 동적 계획법(動的計劃法, dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분
이 문제에 핵심은
1. 2×1과 1×2크기의 타일을 통해 3×n의 벽을 채우는 경우의 수를 구해야 한다.
2. 벽에는 빈 공간이 존재하지 않아야 합니다.
배열
DP[] : 메모이제이션 배열
DP[]배열을 이용하여 벽을 타일로 채우는 모든 경우의 수를 구하였습니다.
DP[i]의 3×i의 벽에 타일을 채우는 경우의 수를 저장합니다.
DP[1~8]까지 표를 표현하면
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| DP값 | 0 | 3 | 0 | 11 | 0 | 41 | 0 | 153 |
DP[2]의 벽을 타일로 채웠을 때 3가지 경우의 수가 도출됩니다.

DP[3]을 살펴보면

위와 같은 형태로 타일을 모두 채울 수 없습니다.
DP[5], DP[7]도 마찬가지로 위와 같은 형태로 벽을 모두 타일로 채울 수 없기 때문에 경우의 수는 0이 됩니다.
결과적으로 DP[i]에서 i가 홀수이면 경우의 수는 0이라는 규칙을 얻습니다.
DP[4]를 살펴보면
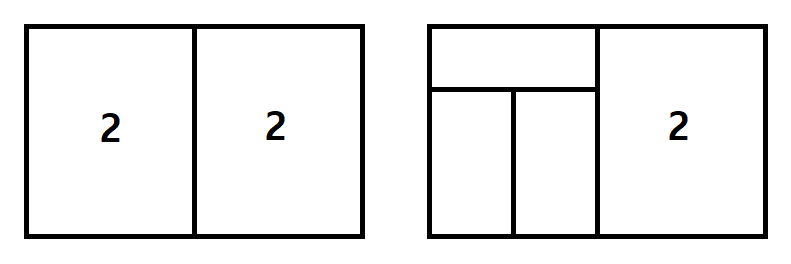
DP[4]의 경우의 수는 DP[2]에서 3×2를 추가한 벽으로 DP[2]의 경우의 수에서 남은 칸 3×2를 채우는 경우의 수를 곱하면 됩니다.
3 × 2를 채우는 경우의 수는 DP[2]로써 3입니다.
결과적으로 위에 과정에서 경우의 수는 DP[2] × DP[2] = 9개입니다.

DP[4]에서 DP[2]에서는 발견하지 못한 특수한 형태도 발견되어 추가합니다.
DP[4] = 9 + 2 = 11
DP[6]을 살펴보면
DP[4]에서 3×2 벽을 추가한 것으로 DP[4]의 경우의 수에서 남은 칸 3×2를 채우는 경우의 수를 곱하면
3 × 2를 채우는 경우의 수는 DP[2]로써 3입니다.
결과적으로 위에 과정에서 경우의 수는 DP[4] × DP[2] = 33개입니다.
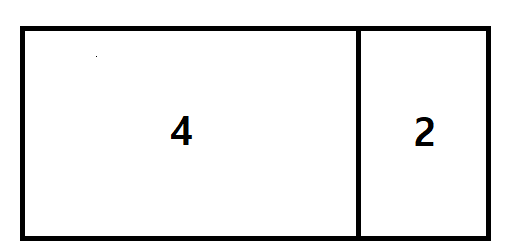
DP[6]에서도 특수한 형태가 발견되는 것을 살펴보면
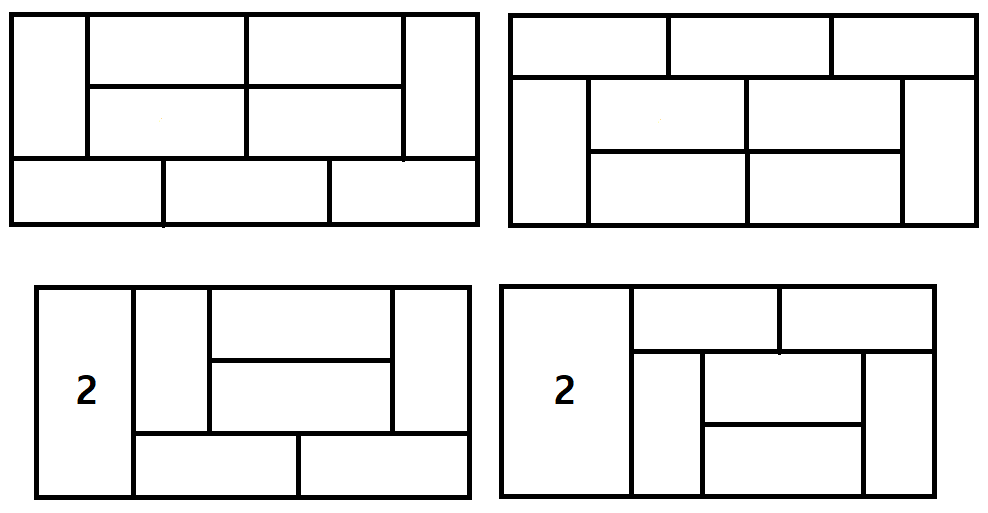
DP[4]일 때 특수한 형태를 이동한 방법과 DP[6]에서의 특수한 형태 2가지의 경우가 나와서
DP[4]의 특수한 형태를 이동한 뒤 3 × 2 벽이 남기 때문에 DP[2]의 경우의 수가 들어갈 수 있습니다.
결과적으로 (DP[2] * 2) + 2 = 8
DP[6] = 33 + 8 = 41
위 과정을 유심히 살펴보면 규칙을 발견할 수 있습니다.
1. DP[i]에서 i가 홀수일 때
DP[i] = 0
2. DP[i]에서 i가 짝수일 때
DP[i] = DP[i-1] × DP[2] + {(DP[i-4] × 2) + (DP[i-6] × 2) + .... + (DP[0] × 2)}로 표현할 수 있습니다.
{(DP[i-4] × 2) + (DP[i-4] × 2) + .... + (DP[0] × 2)} 식은 특수한 형태일 때 경우의 수를 구하는 식입니다.
여기서 DP[0]의 값은 각각의 DP[i]의 특수한 형태는 2개가 존재하기 때문에 DP[0] = 1로 하였습니다.
예를 들어
DP[8]을 구할 때
DP[8] = DP[6] × DP[2] + {(DP[4] × 2) + (DP[2] × 2) + (DP[0] × 2)}
= 41 * 3 + { 22 + 6 + 2} = 123 + 30 = 153
n이 8이면 결과값으로 DP[8]인 153을 결과로 출력하면 됩니다.
문제에 해결알고리즘은
1. DP[0], DP[2]의 값을 1, 3으로 초기화해줍니다.
2. 입력값이 홀수이면 0을 결과로 출력합니다.
3. 입력값이 짝수이면 규칙을 적용하여 DP[]를 구성한 뒤 DP[n]을 결과로 출력합니다.
※DP[2] = 3으로 초기화한 이유는 DP[2]에서는 특수한 형태가 나오지 않기 때문에 위에 규칙이 유효하지 않기 떄문입니다.
- BufferedReader를 사용하여 입력 값을 저장하였습니다.
- DP[0],DP[2]의 값을 1, 3으로 초기화해주었습니다.
- 규칙을 적용하여 DP를 구성하는 cal함수를 만들었습니다.
- BufferedWriter에 입력값이 홀수이면 0을 저장하였습니다.
- BufferedWriter에 입력값이 짝수이면 DP를 구성하여 DP[n]의 값을 저장하였습니다.
- BufferedWriter에 저장된 값을 출력하였습니다.
- cal은 입력값이 짝수일 때 반복문을 통해 위에 설명한 규칙을 적용시켜주었습니다.
결과 코드
import java.io.*;
public class Main{
static int[] DP; //메모이제이션 배열
static int n; //입력값 변수
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
//---------입력값 저장 및 배열 초기화--------
n = Integer.parseInt(br.readLine());
DP = new int[31];
DP[0] = 1;
DP[2] = 3;
if(n%2==1) //규칙1. 홀수일 때
bw.write("0\n");
else { //규칙2. 짝수일 때
cal(); //DP 구성함수 실행
bw.write(DP[n] + "\n"); //DP[n] 값 BufferedWriter 저장
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//------짝수일 때 식을 이용하여 DP를 구성하는 함수-------
static void cal() {
for(int i=2;i<=n;i+=2) {
DP[i] = DP[i-2] * 3; //DP[i-2] × DP[2]
for(int j=i-4;j>=0;j-=2) {
DP[i] += DP[j] * 2; //DP[i-4] × 2 + .... + DP[0] × 2
}
}
return;
}
}'백준' 카테고리의 다른 글
| [백준] code.plus(큐와 그래프,JAVA)10845번, 큐 (0) | 2022.04.20 |
|---|---|
| [백준] 단계별로 풀어보기(단계:25, 최단 경로,JAVA)13549번, 숨바꼭질 3 (0) | 2022.04.19 |
| [백준] 단계별로 풀어보기(단계:27, 동적 계획법과 최단거리 역추적,JAVA)9252번, LCS 2 (0) | 2022.04.17 |
| [백준] code.plus(다이나믹 프로그램 part 2,JAVA)13398번, 연속합 2 (0) | 2022.04.16 |
| [백준] 단계별로 풀어보기(단계:27, 동적 계획법과 최단거리 역추적,JAVA)14003번, 가장 긴 증가하는 부분 수열 5 (0) | 2022.04.15 |




댓글