주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
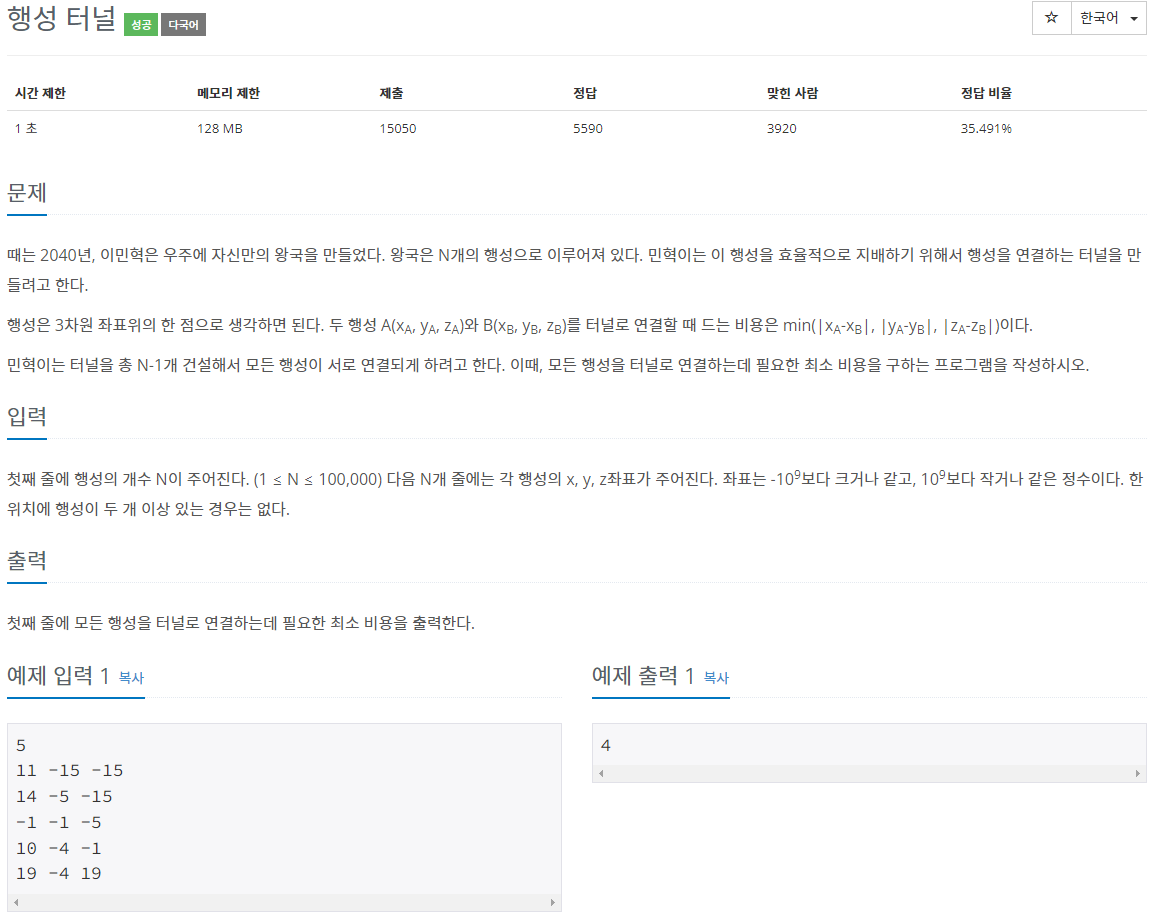
접근 방법
최소 신장 트리
신장 트리 : 어떤 그래프에 대하여 모든 꼭짓점을 포함하는부분 그래프입니다.
최소 신장 트리 : 신장 트리에서 최소의 가중치를 가지는 부분 그래프입니다.
Minimum spanning tree - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Tree of smallest total weight through all vertices of a graph A planar graph and its minimum spanning tree. Each edge is labeled with its weight, which here is roughly proportional to
en.wikipedia.org
이 문제에 핵심은
1. 입력되는 값은 행성의 x, y, z 좌표입니다.
2. 모든 행성이 연결되며 터널의 가중치가 최소인 값을 결과로 출력해야 합니다.
3. 행성간 연결하는 터널의 거리는 일반적인 3차원 좌표 거리 공식이 아닙니다.
최소 신장 트리를 구하기 위해서 Union-Find와 Greedy알고리즘을 이용하여 구현하였습니다.
Union Find - 나무위키
Disjoint Set에서는 트리를 특이한 용도로 사용하는데, 트리의 구조 자체가 의미를 가지는 경우가 많은 반면 Disjoint Set에서는 트리의 구조와는 상관 없이 단 하나의 최상위 노드에만 관심을 가진다.
namu.wiki
탐욕 알고리즘 - 위키백과, 우리 모두의 백과사전
탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인
ko.wikipedia.org
Greedy알고리즘을 이용하여 가중치가 낮은 선분부터 탐색을 시작합니다.
선분을 탐색할 때 Union-Find를 이용하여 사이클이 발생하는지 확인하여 최소 신장 트리를 완성하였습니다.
선분에 대한 정보를 얻기 위해서 각 행성에 대하여 나올 수 있는 통로를 모두 구해서 최소 신장 트리를 구하였지만
결과는 "메모리 초과" 였습니다.
이유를 생각해보니 모든 경우의 통로를 구하면 주어진 행성의 수가 100,000개일 때 모든 통로를 구하면 100000!개 필요하기 때문에 "메모리 초과"가 발생할 수 밖에 없다고 생각되었습니다.
문제에서 각 터널의 길이는
min(|x1-x2|, |y1-y2|, |z1-z2|)
최소 신장 트리에서 나올 수 있는 통로의 길이는 x축 기준 최소 신장 트리, y축 기준 최소 신장 트리, z축 기준 최소 신장 트리에 사용하였던 선분만을 사용합니다.
x, y, z축 기준 최소 신장 트리를 구하려면
각 축을 기준으로 오름차순으로 정렬한 뒤에
각 행성들을 순차적으로 연결하면 해당 축을 기준으로 한 최소 신장 트리를 구할 수 있습니다.
각 축을 기준으로 얻은 최소 신장 트리에 사용될 통로들과 Union-Find를 이용해서 최소 신장 트리를 구현하여 가중치의 합을 결과로 출력하였습니다.
예제입력1
각 행성의 위치를 X축 기준 정렬
| 3번째 행성 | 4번째 행성 | 1번째 행성 | 2번째 행성 | 5번째 행성 |
| -1 | 10 | 11 | 14 | 19 |
3 -> 4, 길이 : 11
4 -> 1, 길이 : 1
1 -> 2, 길이 : 3
2 -> 5, 길이 : 5
각 행성의 위치를 Y축 기준 정렬
| 1번째 행성 | 2번째 행성 | 4번째 행성 | 5번째 행성 | 3번째 행성 |
| -15 | -5 | -4 | -4 | -1 |
1 -> 2, 길이 : 10
2 -> 4, 길이 : 1
4 -> 5, 길이 : 0
5 -> 3, 길이 : 3
각 행성의 위치를 Z축 기준 정렬
| 1번째 행성 | 2번째 행성 | 3번째 행성 | 4번째 행성 | 5번째 행성 |
| -15 | -15 | -5 | -1 | 19 |
1 -> 2, 길이 : 0
2 -> 3, 길이 : 10
3 -> 4, 길이 : 4
4 -> 5, 길이 : 20
Union-Find를 사용하기 위해 축을 기준으로 얻은 통로들을 오름차순으로 정렬
1 -> 2, 길이 : 0
4 -> 5, 길이 : 0
4 -> 1, 길이 : 1
2 -> 4, 길이 : 1
1 -> 2, 길이 : 3
5 -> 3, 길이 : 3
3 -> 4, 길이 : 4
2 -> 5, 길이 : 5
1 -> 2, 길이 : 10
2 -> 3, 길이 : 10
3 -> 4, 길이 : 11
4 -> 5, 길이 : 20
Union-Find에 사용할 Root Node 가리키는 값
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
1 - 2. 탐색
1과 2의 Root Node는 다르기 때문에 사이클 형성 X, 선분을 이용
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 3 | 4 | 5 |
4 - 5. 탐색
4와 5의 Root Node는 다르기 때문에 사이클 형성 X, 선분을 이용
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 3 | 4 | 4 |
4 - 1. 탐색
4와 1의 Root Node는 다르기 때문에 사이클 형성 X, 선분을 이용
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 3 | 1 | 4 |
2 - 4. 탐색
2와 4의 Root Node는 같기 때문에 사이클 형성 O, 선분을 이용X
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 3 | 1 | 4 |
1 - 2. 탐색
1과 2의 Root Node는 같기 때문에 사이클 형성 O, 선분을 이용X
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 3 | 1 | 4 |
5 - 3. 탐색
5와 3의 Root Node는 다르기 때문에 사이클 형성 X, 선분을 이용
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 |
사용되는 통로 1 - 2, 4 - 5, 4 - 1, 5 - 3의 가중치의 합은 = 0 + 0 + 1 + 3 = 4
최소 신장 트리의 가중치의 합(4)을 결과로 출력합니다.
- BufferedReader를 사용하여 입력 값을 저장하였습니다.
- StringTokenizer를 사용하여 행성에 x, y, z좌표를 저장합니다.
- 각 축을 기준으로 정렬하는 sortX/sortY/sortZ 실행하였습니다.
- 각 축으로 정렬한 뒤 해당 기준 최소 신장 트리에 사용되는 통로를 구하였습니다.
- 최소 신장 트리에 사용되는 통로와 union함수를 이용하여 사이클이 생기지 않는 선분의 가중치들을 더하였습니다.
- BufferedWriter에 최소 신장 트리의 가중치 합을 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- sortX/sortY/sortZ함수는 Arrays.sort()을 이용하여 각 축을 기준으로 오름차순 정렬합니다.
- sortTunnel함수는 Collections.sort()을 이용하여 터널의 거리를 기준으로 오름차순 정렬합니다.
- find함수는 루트 노드의 값을 구하는 재귀 함수입니다.
- union함수는 루트 노드가 같은지 확인 및 변경하는 함수입니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
//행성의 좌표 생성자
static class coordinate{
int n, x, y, z;
public coordinate(int n, int x, int y, int z) {
super();
this.n = n;
this.x = x;
this.y = y;
this.z = z;
}
}
//통로 생성자
static class tunnel{
int p1, p2, width;
public tunnel(int p1, int p2, int width) {
super();
this.p1 = p1;
this.p2 = p2;
this.width = width;
}
}
static int N;
static coordinate[] planet; //행성의 좌표 저장 배열
static ArrayList<tunnel> line = new ArrayList<>(); //행성간 통로 저장 리스트
static int[] root; //루트 노드 저장 배열
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
StringTokenizer st;
N = Integer.parseInt(br.readLine());
planet = new coordinate[N];
root = new int[N];
//루트 노드 초기화
for(int i=0;i<N;i++)
root[i] = i;
//행성 좌표 저장
for(int i=0;i<N;i++) {
st = new StringTokenizer(br.readLine()," ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
int z = Integer.parseInt(st.nextToken());
planet[i] = new coordinate(i, x, y, z);
}
//X축 기준 최소 신장 트리에 사용되는 통로 구하기
sortX(); //X축 오름차순 정렬
for(int i=0;i<N-1;i++)
line.add(new tunnel(planet[i].n, planet[i+1].n, Math.abs(planet[i].x-planet[i+1].x)));
//Y축 기준 최소 신장 트리에 사용되는 통로 구하기
sortY(); //Y축 오름차순 정렬
for(int i=0;i<N-1;i++)
line.add(new tunnel(planet[i].n, planet[i+1].n, Math.abs(planet[i].y-planet[i+1].y)));
//Z축 기준 최소 신장 트리에 사용되는 통로 구하기
sortZ(); //Z축 오름차순 정렬
for(int i=0;i<N-1;i++)
line.add(new tunnel(planet[i].n, planet[i+1].n, Math.abs(planet[i].z-planet[i+1].z)));
sortTunnel(); //모든 통로 오름차순 정렬
long result = 0;
//최소 신장 트리의 가중치 구하기
for(int i=0;i<line.size();i++) {
if(!union(line.get(i).p1, line.get(i).p2)) {
result += line.get(i).width;
}
}
bw.write(result + "\n"); //가중치 결과 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//루트 노드 찾는 함수
static int find(int n) {
if(n==root[n])
return n;
return root[n] = find(root[n]);
}
//루트 노드 같은지 확인 및 변경하는 함수
static boolean union(int a, int b) {
int x = find(a);
int y = find(b);
if(x!=y) {
if(x>y)
root[x] = y;
else
root[y] = x;
return false;
}
return true;
}
//행성 좌표 X축 기준 정렬 함수
static void sortX() {
Arrays.sort(planet, new Comparator<coordinate>(){
@Override
public int compare(coordinate o1, coordinate o2) {
return o1.x - o2.x;
}
});
}
//행성 좌표 Y축 기준 정렬 함수
static void sortY() {
Arrays.sort(planet, new Comparator<coordinate>(){
@Override
public int compare(coordinate o1, coordinate o2) {
return o1.y - o2.y;
}
});
}
//행성 좌표 Z축 기준 정렬 함수
static void sortZ() {
Arrays.sort(planet, new Comparator<coordinate>(){
@Override
public int compare(coordinate o1, coordinate o2) {
return o1.z - o2.z;
}
});
}
//터널 길이 기준 정렬 함수
static void sortTunnel() {
Collections.sort(line,new Comparator<tunnel>() {
@Override
public int compare(tunnel o1, tunnel o2) {
return o1.width - o2.width;
}
});
}
}'백준' 카테고리의 다른 글
| [백준] 단계별로 풀어보기(단계:31, 최소 신장 트리,JAVA)17472번, 다리 만들기 2 (0) | 2022.06.13 |
|---|---|
| [백준] code.plus(그래프 알고리즘,JAVA)16947번, 서울 지하철 2호 (0) | 2022.06.13 |
| [백준] code.plus(그래프 알고리즘,JAVA)16929번, Two Dots (0) | 2022.06.11 |
| [백준] 단계별로 풀어보기(단계:31, 최소 신장 트리,JAVA)1774번, 우주신과의 교감 (0) | 2022.06.10 |
| [백준] code.plus(브루트포스 - 기타,JAVA)2143번, 두 배열의 합 (0) | 2022.06.10 |




댓글