주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
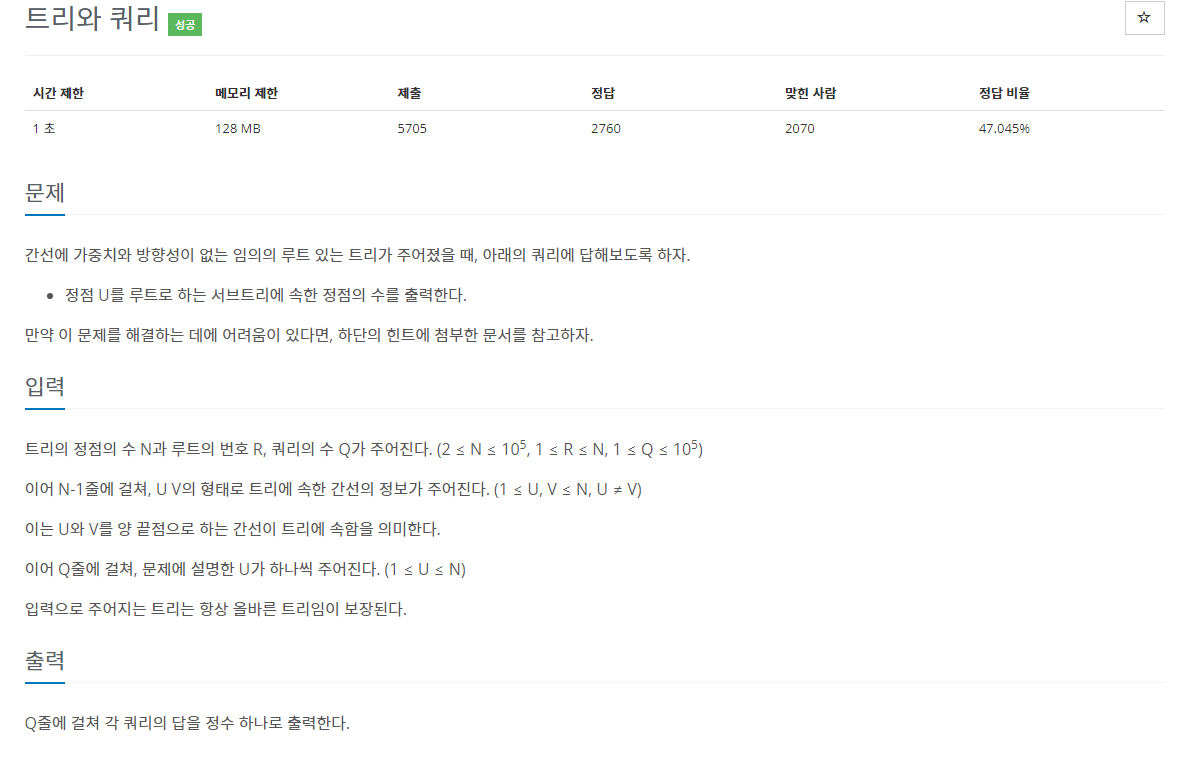

접근 방법
트리
서로 다른 두 노드를 잇는 길이 하나뿐인 그래프(사이클 X)
트리 구조 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
동적계획법
동일한 연산을 계속 반복하여 비효율적으로 코드가 실행되어 그것을 향상시키기 위하여 반복되는 연산의 결과를 따로 저장하여 적재적소에 코드가 더 효율적으로 만드는 방법입니다.
이 문제에 핵심은
1. 임의의 루트 트리가 주어진다.
2. 정점 U에 대한 서브 트리에 정점 개수를 결과로 출력한다.
입력받은 루트 노드를 기준으로 하위 노드로 넘어가면서 존재하는 정점의 수를 DP[]에 저장하였습니다.
이후 Q개의 U의 대해서 DP[U]의 값을 결과로 출력하였습니다.
예제입력1
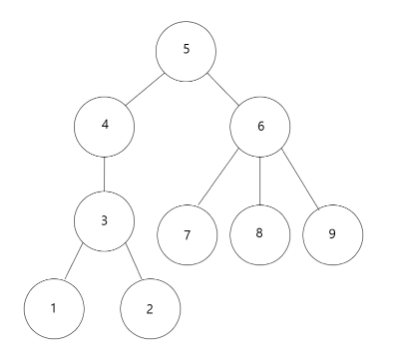
루트 노드 5부터 재귀를 통해 해당 서브 트리의 정점의 수를 저장하면
DP[1] = 1
DP[2] = 1
DP[3] = DP[1] + DP[2] + 1 = 1 + 1 + 1 = 3
DP[4] = DP[3] + 1 = 3 + 1 = 4
DP[7] = 1
DP[8] = 1
DP[9] = 1
DP[6] = DP[7] + DP[8] + DP[9] + 1 = 1 + 1 + 1 + 1 = 4
DP[5] = DP[4] + DP[6] + 1 = 4 + 4 + 1 = 9
Q개의 U를 입력받는다.
U = 5
DP[5] = 9
U = 4
DP[4] = 4
U = 8
DP[8] = 1
9, 4, 1을 결과로 출력합니다.
- BufferedReader를 사용하여 입력 값을 저장하였습니다.
- StringTokenizer를 사용하여 트리에 대한 정보를 저장합니다.
- 루트 노드를 시작으로 서브 트리의 정점의 수를 탐색하는 search함수를 실행하였습니다.
- BufferedWriter에 Q개에 U의 값에 따른 DP값을 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- search함수는 루트 노드를 기준으로 하위 트리의 속한 정점의 수를 DP에 저장하는 재귀 함수입니다.
- search함수는 DP를 이용해서 탐색을 진행했다면 DP값을 가져오도록 하였습니다.
결과 코드
import java.io.*;
import java.util.*;
public class Main{
static int N,R,Q;
static int[] DP; //서브 트리 정점 수 저장 메모이제이션
static ArrayList<ArrayList<Integer>> graph = new ArrayList<>(); //트리 정보 저장 리스트
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
R = Integer.parseInt(st.nextToken());
Q = Integer.parseInt(st.nextToken());
DP = new int[N+1];
for(int i=0;i<=N;i++) {
graph.add(new ArrayList<>());
}
//입력되는 트리 저장
for(int i=0;i<N-1;i++) {
st = new StringTokenizer(br.readLine()," ");
int U = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
graph.get(U).add(V);
graph.get(V).add(U);
}
search(R , 0); //루트 노드 기준 재귀 탐색 진행
//Q개의 U에 대하여 DP값 BufferedWriter 저장
for(int i=0;i<Q;i++) {
int num = Integer.parseInt(br.readLine());
bw.write(DP[num] + "\n");
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//루트 노드를 시작으로 재귀를 통해 서브 트리의 정점의 수 DP에 저장하는 재귀 함수
static int search(int root, int parent) {
if(DP[root]!=0) //이미 탐색한 정점일 때
return DP[root];
DP[root] = 1; //자기 자신 정점 + 1
for(int next : graph.get(root)) {
if(next != parent) { //부모 정점을 제외한 연결된 정점 탐색
DP[root] += search(next,root);
}
}
return DP[root];
}
}'백준' 카테고리의 다른 글
| [백준] code.plus(그래프 알고리즘,JAVA)16964번, DFS 스페셜 저지 (0) | 2022.06.16 |
|---|---|
| [백준] code.plus(그래프 알고리즘,JAVA)16940번, BFS 스페셜 저지 (0) | 2022.06.16 |
| [백준] code.plus(그래프 알고리즘,JAVA)12946번, 육각 보드 (0) | 2022.06.15 |
| [백준] 단계별로 풀어보기(단계:31, 최소 신장 트리,JAVA)17472번, 다리 만들기 2 (0) | 2022.06.13 |
| [백준] code.plus(그래프 알고리즘,JAVA)16947번, 서울 지하철 2호 (0) | 2022.06.13 |




댓글