문제 링크
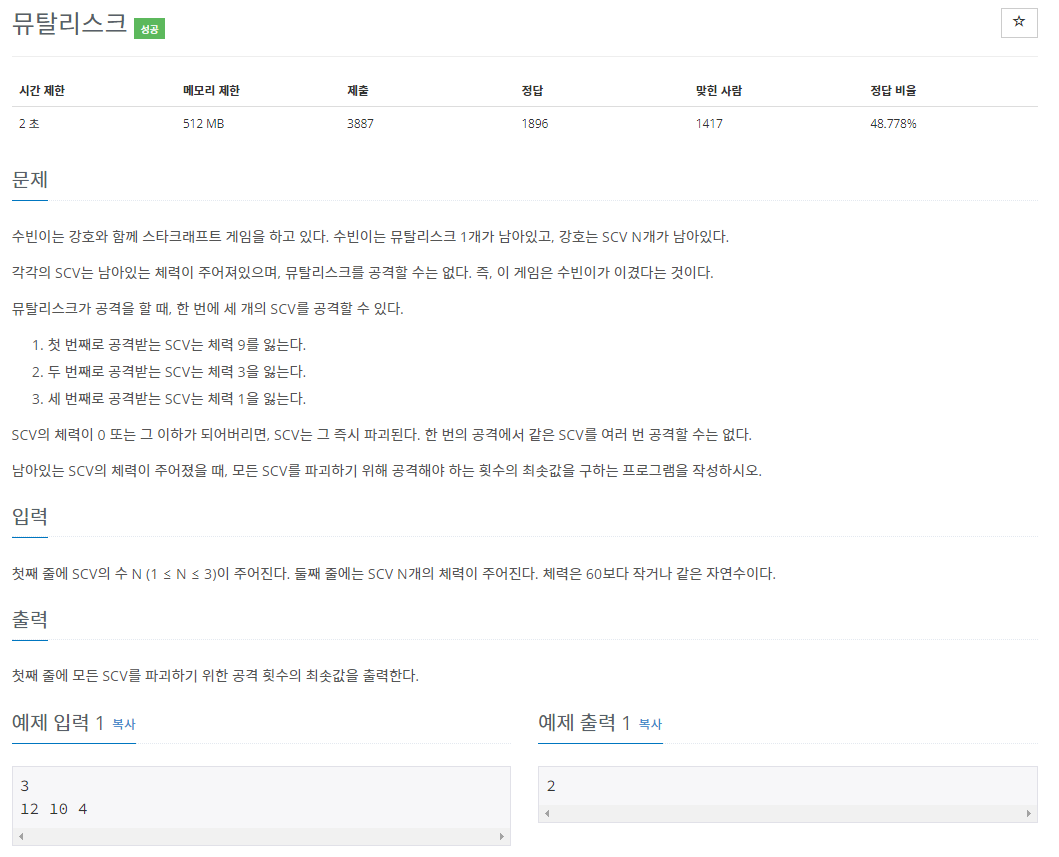
12869번: 뮤탈리스크
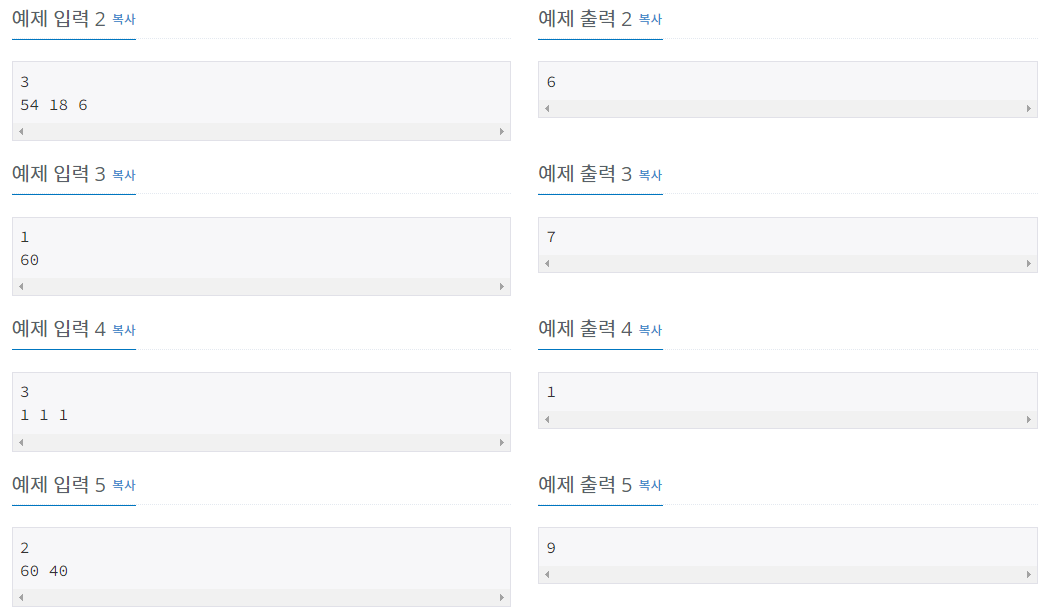
1, 3, 2 순서대로 공격을 하면, 남은 체력은 (12-9, 10-1, 4-3) = (3, 9, 1)이다. 2, 1, 3 순서대로 공격을 하면, 남은 체력은 (0, 0, 0)이다.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
동적 계획법
모든 연산을 수행하면 똑같은 연산을 중복되게 수행하게 되는데 다이나믹 프로그램은 연산한 내용을 따로 저장하여 효율적으로 작성한 프로그램입니다.
이 문제에 핵심은
1. 뮤탈리스크는 공격은 -9, -3, -1으로 3개의 scv를 공격할 수 있다.
2. scv의 체력이 0미만으로 내려가면 0으로 고정됩니다.
3. scv의 개수는 최대 3개이며 scv를 모두 파괴하는 최소 공격 횟수를 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력되는 scv에 대한 정보를 저장합니다.
2. 뮤탈리스크의 공격의 경우의 수를 탐색하여 DP[][]에 저장합니다.
3. DP[scv1][scv2][scv3]의 값을 결과로 출력합니다.
DP[i][j][s]의 형태
scv에 체력을 내림차순으로 정렬하여 순서대로 입력한 배열의 값
Ex.
scv1 - 5
scv2 - 15
scv3 - 8
DP[15][8][5]의 값에 저장된다.
뮤탈리스크의 공격의 경우의 수
{9, 3, 1} : scv1(-9), scv2(-3), scv3(-1)
{9, 1, 3} : scv1(-9), scv2(-1), scv3(-3)
{3, 9, 1} : scv1(-3), scv2(-9), scv3(-1)
{3, 1, 9} : scv1(-3), scv2(-1), scv3(-9)
{1, 9, 3} : scv1(-1), scv2(-9), scv3(-3)
{1, 3, 9} : scv1(-1), scv2(-3), scv3(-9)
예제입력 1.
1. 입력되는 scv에 대한 정보를 저장합니다.
N = 3
scv의 체력 - 12, 10, 4
2. 뮤탈리스크의 공격의 경우의 수를 탐색하여 DP[][]에 저장합니다.
현재 scv의 체력을 내림차순 정렬
scv1 : 12
scv2 : 10
scv3 : 4
뮤탈리스크 공격!
{9, 3, 1}
scv1 : 3
scv2 : 7
scv3 : 3
{9, 1, 3}
scv1 : 3
scv2 : 9
scv3 : 1
{3, 9, 1}
scv1 : 9
scv2 : 3
scv3 : 3
{3, 1, 9}
scv1 : 9
scv2 : 9
scv3 : 0
{1, 9, 3}
scv1 : 11
scv2 : 1
scv3 : 1
{1, 3, 9}
scv1 : 11
scv2 : 7
scv3 : 0
DP[12][10][4]에 위에 공격의 최소값을 저장합니다.
.....뮤탈리스크 공격 진행
3. DP[scv1][scv2][scv3]의 값을 결과로 출력합니다.
DP[12][10][4] = 2을 결과로 출력합니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- StringTokenizer을 이용하여 SCV에 대한 정보를 저장하였습니다.
- search함수를 실행하여 최소 공격 횟수를 BufferedWriter에 저장합니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- search는 재귀와 DP를 통해서 뮤탈리르크의 공격을 진행합니다.
- search는 DP에 뮤탈리스크 최소 공격 횟수를 저장합니다.
import java.util.*;
import java.io.*;
public class Main {
static int N;
static int [][][] DP = new int[61][61][61];
//뮤탈의 공격 경우의 수
static int[][] attack = { {9, 3, 1}, {9, 1, 3}, {3, 9, 1}, {3, 1, 9}, {1, 9, 3}, {1, 3, 9}};
static Integer[] scv = new Integer[3]; //scv 체력 저장 배열
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(br.readLine());
//DP[][][] 초기화
for(int i=0;i<61;i++){
for(int j=0;j<61;j++)
Arrays.fill(DP[i][j], Integer.MAX_VALUE);
}
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//입력되는 SCV 체력 저장
for(int i=0;i<N;i++)
scv[i] = Integer.parseInt(st.nextToken());
//SCV의 개수가 3개 미만인 경우 없는 SCV의 체력 0으로 초기화
for(int i=N;i<3;i++)
scv[i] = 0;
bw.write(search(scv.clone(),0) + ""); //최소 공격횟수 구하기 및 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//뮤탈리스크 공격 경우의 수와 DP를 이용하여 최소 공격횟수 구하는 함수
static int search(Integer[] scv, int count){
boolean check = false;
for(int i=0;i<N;i++){ //모든 SCV가 체력이 0일 때
if(scv[i]!=0){
check = true;
break;
}
}
if(!check){ //모든 SCV가 체력이 0일 때
return count;
}else{ //모든 SCV가 체력이 0이 아닐 때
Arrays.sort(scv, Collections.reverseOrder()); //SCV 체력 내림차순 정렬
//먼저 방문했을 경우 해당 값 반환
if(DP[scv[0]][scv[1]][scv[2]]!=Integer.MAX_VALUE)
return DP[scv[0]][scv[1]][scv[2]];
//뮤탈리스크 공격 진행!
for(int i=0;i<6;i++){
Integer[] tempScv = new Integer[3];
tempScv[0] = Math.max(scv[0] - attack[i][0], 0);
tempScv[1] = Math.max(scv[1] - attack[i][1], 0);
tempScv[2] = Math.max(scv[2] - attack[i][2], 0);
//모든 공격의 최소값 DP의 저장
DP[scv[0]][scv[1]][scv[2]] = Math.min(DP[scv[0]][scv[1]][scv[2]], search(tempScv, count+1));
}
}
return DP[scv[0]][scv[1]][scv[2]];
}
}'백준' 카테고리의 다른 글
| [백준] code.plus(다이나믹 프로그래밍,JAVA)2294번, 동전 2 (0) | 2022.08.01 |
|---|---|
| [백준] code.plus(다이나믹 프로그래밍,JAVA)10422번, 괄호 (0) | 2022.07.31 |
| [백준] code.plus(다이나믹 프로그래밍,JAVA)1495번, 기타리스트 (0) | 2022.07.29 |
| [백준] code.plus(다이나믹 프로그래밍,JAVA)15989번, 1, 2, 3 더하기 4 (0) | 2022.07.28 |
| [백준] code.plus(다이나믹 프로그래밍,JAVA)11060번, 점프 점프 (0) | 2022.07.27 |




댓글