문제 링크
17085번: 십자가 2개 놓기
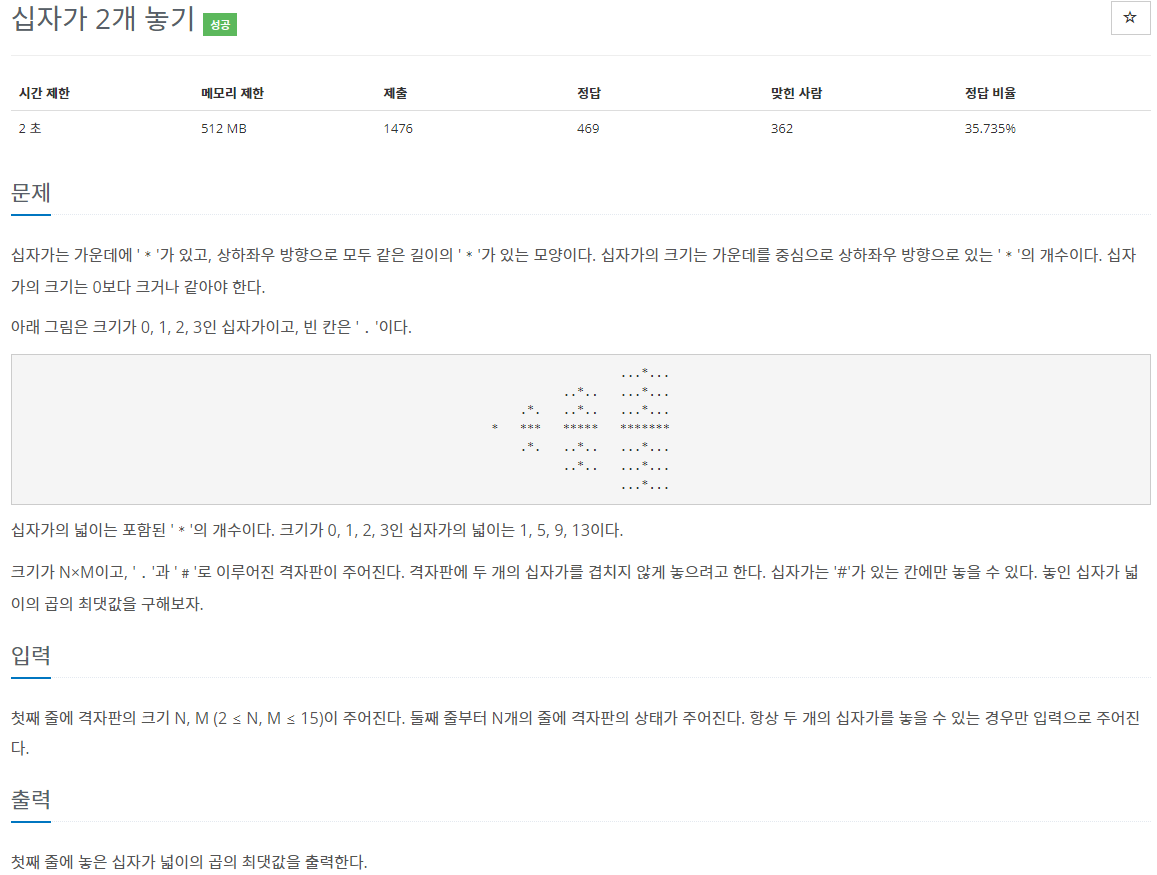
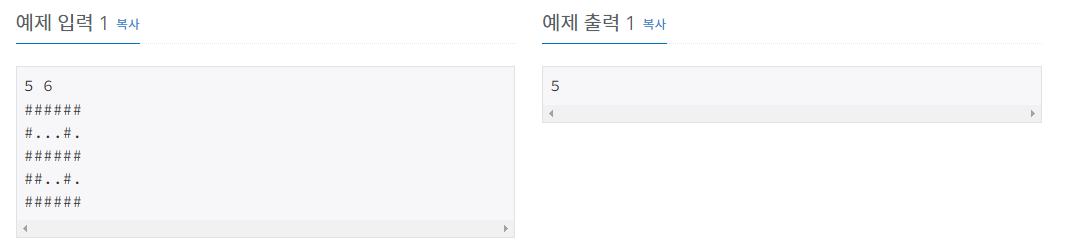
첫째 줄에 격자판의 크기 N, M (2 ≤ N, M ≤ 15)이 주어진다. 둘째 줄부터 N개의 줄에 격자판의 상태가 주어진다. 항상 두 개의 십자가를 놓을 수 있는 경우만 입력으로 주어진다.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
이 문제에 핵심
1. 십자가의 크기는 0부터 시작합니다.
2. 십자가가 놓일 수 있는 칸은 '#'으로 표현됩니다.
3. 격자판에 2개의 십자가를 놓을 때 십자가들의 넓이의 곱의 최대값을 결과로 출력합니다.
4. 십자가는 중복된 칸에 놓을 수 없습니다.
알고리즘 진행 순서.
1. 입력되는 정보들을 저장합니다.
2. 십자가를 놓는 모든 경우를 탐색합니다.
3. 모든 경우 탐색 후 놓인 2개의 십자가 넓이의 곱의 최대값을 결과로 출력합니다.
십자가 놓기
※ 십자가를 놓을 수 있는 칸에는 최대의 십자가 크기가 아닌 놓일 수 있는 크기를 모두 탐색해야 합니다.
1번째 십자가 놓기
격자판에 있는 '#'을 찾아서 놓일 수 있는 모든 크기의 십자가를 선택합니다.
2번째 십자가 놓기
1번째 십자가가 놓인 격자판에서 놓을 수 있는 가장 크기가 큰 십자가를 찾습니다.
십자가 넓이 구하는 점화식
십자가 크기 × 4 + 1
예제입력 2.
1. 입력되는 정보들을 저장합니다.
N=6, M = 6
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
2. 십자가를 놓는 모든 경우를 탐색합니다.
※2가지 경우만 탐색하는 과정을 보여드리겠습니다.
(0, 1)기준
첫 번째 십자가 놓기
(0, 0)에서 놓을 수 있는 십자가의 크기는 1개(0)이 있습니다.
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
두 번째 십자가 놓기
첫 번째 십자가를 놓은 환경에서
격자판에서 놓을 수 있는 십자가의 최대 크기를 구합니다.
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
두 십자가의 넓이의 곱은 1 × 5 = 5
(1, 1)기준
첫 번째 십자가 놓기
(0, 0)에서 놓을 수 있는 십자가의 크기는 2개(0, 1)이 있습니다.
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
첫 번째 십자가의 크기가 0일 때 두 번째 십자가 놓기
첫 번째 십자가(크기 : 0)를 놓은 환경에서
격자판에서 놓을 수 있는 십자가의 최대 크기를 구합니다.
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
두 십자가의 넓이의 곱은 1 × 5 = 5
첫 번째 십자가의 크기가 1일 때 두 번째 십자가 놓기
첫 번째 십자가(크기 : 1)를 놓은 환경에서
격자판에서 놓을 수 있는 십자가의 최대 크기를 구합니다.
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| # | # | # | # | # | # |
| . | # | . | . | # | . |
| . | # | . | . | # | . |
두 십자가의 넓이의 곱은 5 × 5 = 25
3. 모든 경우 탐색 후 식의 최대값을 결과로 출력합니다.
최대값 25를 결과로 출력합니다.
- BufferedReader를 사용하여 입력 값을 받았습니다.
- StringTokenizer를 이용하여 N, M을 띄어쓰기 기준 나누었습니다.
- for문와 crossCheck를 통해서 격자판에 첫 번째 십자가가 놓일 수 있는 크기들을 찾습니다.
- 첫 번째 십자가의 크기들에서 search을 이용해서 두 번째 십자가의 가장 큰 크기를 놓았습니다.
- 십자가를 놓는 모든 경우 탐색 후 두 십자가의 곱의 최대값을 BufferedWriter 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- search함수는 첫 번째 십자가가 주어진 환경에서 두 번째 십자가의 최대 크기를 탐색합니다.
- crossCheck함수는 첫 번째 십자가가 여러 크기들이 놓일 수 있는지 확인합니다.
- crossMaxSizeCheck함수는 입력받은 기준으로 놓을 수 있는 십자가의 최대 크기를 구합니다.
- crossSize함수는 십자가의 크기가 주어졌을 때 넓이를 구합니다.
- inSpace함수는 이동하려는 칸이 격자판 안에 존재하는지 확인합니다.
import java.io.*;
import java.util.*;
public class Main {
static int N,M, answer = 1;
static char[][] map; //격자판 정보
static boolean[][] visited; //십자가 놓인 곳 확인 배열
static int[] dx = {0, 0, -1, 1}; //상하좌우 x변경값
static int[] dy = {-1, 1, 0, 0}; //상하좌우 y변경값
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
map = new char[N][M];
//격자판 정보 저장
for(int i=0;i<N;i++){
String str = br.readLine();
for(int j=0;j<M;j++)
map[i][j] = str.charAt(j);
}
//첫 번째 십자가 놓기
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
if(map[i][j] == '#'){
visited = new boolean[N][M];
int temp = Math.max(i,j); //놓일 수 있는 최대 십자가 크기
for(int s=0;s<=temp;s++){
//해당 크기의 십자가 격자판에 놓일 수 있는지 확인
if(!crossCheck(i, j ,s))
break;
search(i, j, s); //놓일 수 있을 때 두 번째 십자가 탐색
}
}
}
}
bw.write(answer + ""); //두 십자가 넓이의 곱의 최대값 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//입력받은 좌표에서 해당 크기에 십자가 놓을 수 있는지 확인하는 함수
static boolean crossCheck(int y, int x, int size){
for(int i=0;i<4;i++){
int tempX = x + dx[i] * size;
int tempY = y + dy[i] * size;
//해당 크기에 십자가 놓을 수 없을 때
if(!inSpace(tempX ,tempY) || map[tempY][tempX] !='#'){
return false;
}
}
visited[y+size][x] = visited[y-size][x] = visited[y][x+size] = visited[y][x-size] = true;
return true;
}
//해당 좌표에서 놓을 수 있는 십자가의 최대 크기를 구하는 함수
static int crossMaxSizeCheck(int y, int x){
int result = 1;
while(true){
boolean check = false;
//십자가 기준 상하좌우 탐색
for(int i=0;i<4;i++){
int tempX = x + dx[i] * result;
int tempY = y + dy[i] * result;
//십자가 더 이상 크기 넓히지 못할 때
if(!inSpace(tempX,tempY) || map[tempY][tempX]!='#' || visited[tempY][tempX]){
check = true;
break;
}
}
if(check)
break;
result++;
}
return result-1;
}
//첫 번째 십자가가 놓인 환경에서 두 번째 십자가의 최대 크기 탐색하는 함수
static void search(int y, int x, int size){
int result = 0;
for(int i=x+1;i<M;i++){
if(map[y][i]=='#'){
result = Math.max(result, crossMaxSizeCheck(y, i));
}
}
for(int i=y+1;i<N;i++){
for(int j=0;j<M;j++){
if(map[i][j]=='#'){
result = Math.max(result, crossMaxSizeCheck(i, j));
}
}
}
//(첫 번째 십자가 넓이 × 두 번째 십자가 넓이)가 최대값인지 비교
answer = Math.max(answer, crossSize(size) * crossSize(result));
}
//십자가 크기에 따른 넓이 구하는 함수
static int crossSize(int size){
return size * 4 + 1; //점화식 : 크기 × 4 + 1
}
//이동하려는 칸이 격자판 안에 존재하는지 확인하는 함수
static boolean inSpace(int x, int y){
//격자판 안에 존재하는 공간일 때
if(x>=0 && y>=0 && x<M && y<N)
return true;
return false;
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(문자열,JAVA)1439번, 뒤집기 (2) | 2022.09.15 |
|---|---|
| [백준] code.plus(브루트 포스 Part 2,JAVA)17825번, 주사위 윷놀이 (0) | 2022.09.08 |
| [백준] code.plus(브루트 포스 Part 2,JAVA)16638번, 괄호 추가하기 2 (0) | 2022.09.06 |
| [백준] code.plus(브루트 포스 Part 2,JAVA)17069번, 파이프 옮기기 2 (0) | 2022.09.05 |
| [백준] code.plus(브루트 포스 Part 2,JAVA)17070번, 파이프 옮기기 1 (0) | 2022.09.04 |




댓글