문제 링크
1916번: 최소비용 구하기
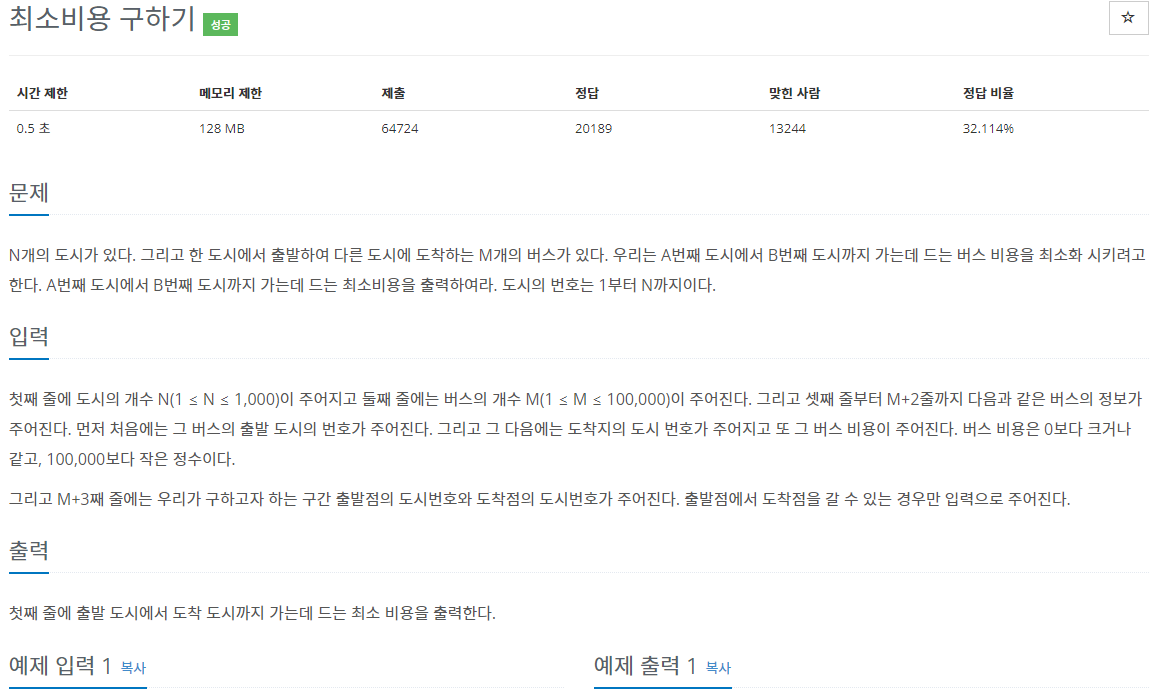
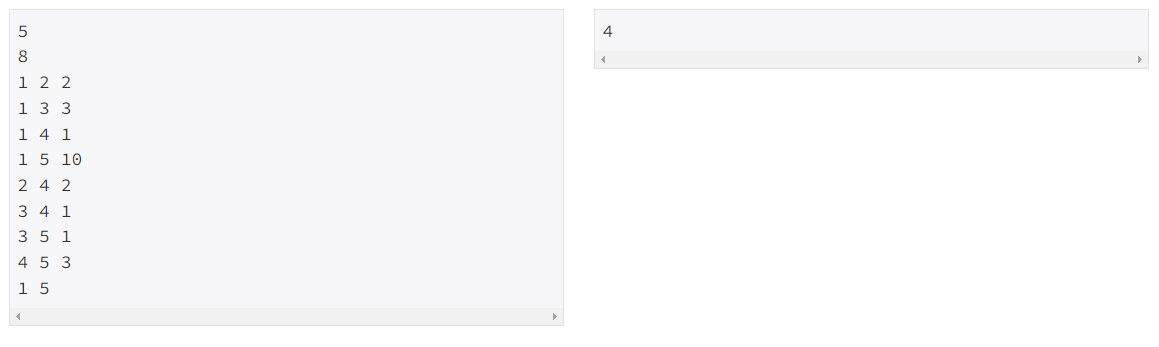
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. 버스는 방향이 존재하는 간선입니다.
2. 도시의 번호는 1~N번까지 존재합니다.
3. A번째 도시에서 B번째 도시에 도착하는 최소 비용을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. A번째 도시에서 B번째 도시에 최단 거리를 탐색합니다.
3. 탐색을 통해 얻은 최소 비용을 결과를 출력합니다.
최단 거리 알고리즘
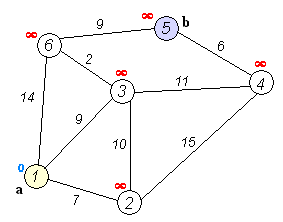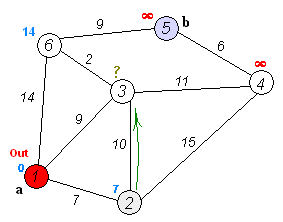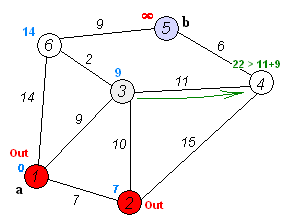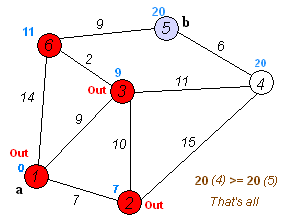
1. 출발 정점에서 인접한 정점으로 이동합니다.
2. 인접한 정점에서 가장 적은 가중치(거리)의 정점을 먼저 탐색합니다.
3. 이동을 할 때마다 이동한 거리가 현재 저장된 거리보다 작으면 변경합니다.
4. 위 과정을 반복이 끝나면 출발 정점에서 각 정점에 도착하는 최소 거리을 구할 수 있습니다.
글로는 잘 설명하지 못한 것 같아서 아래에 예제 문제를 풀면서 어떻게 진행되는지 자세히 보여드리겠습니다.
더 자세한 내용은 아래 링크를 통해 확인해주시기 바랍니다.
데이크스트라 알고리즘 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서, 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.
ko.wikipedia.org
각 도시마다 버스의 대한 정보를 ArrayList<ArrayList<>>()의 그래프 형태로 저장되도록 하였습니다.
최단 경로 구하는 과정을 BFS에 PriorityQueue<>을 이용해서 구현하였습니다.
최단 경로 구하는 과정은 예제입력 진행되는 과정을 보시면 이해하시는데 도움이 될 것입니다.
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 5
M : 8
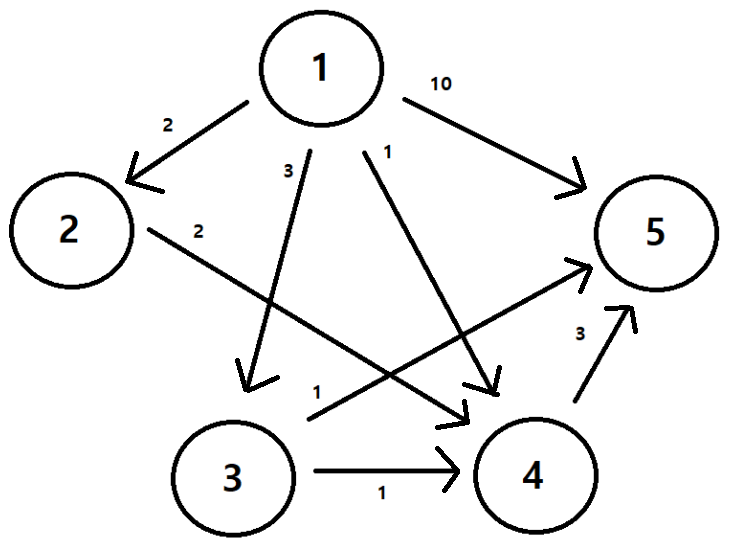
2. A번째 도시에서 B번째 도시에 최단 거리를 탐색합니다.
1번째 도시에서 5번째 도시 최단 거리 탐색!
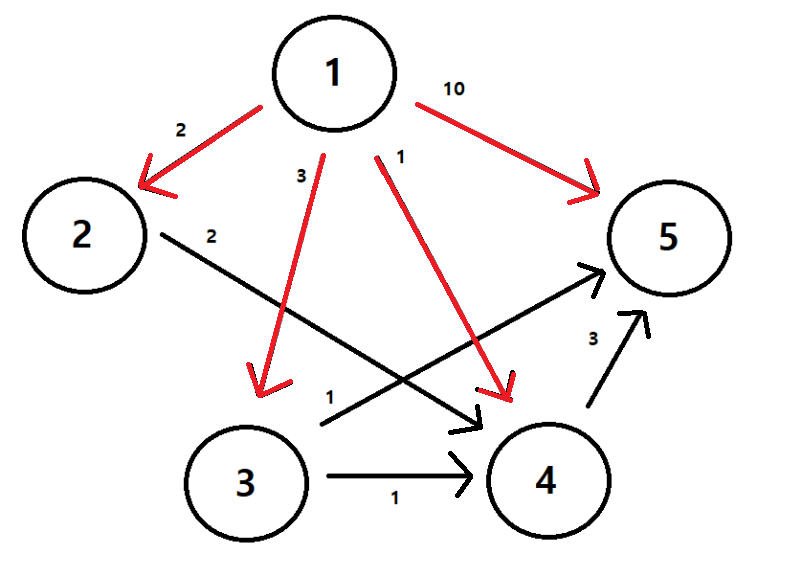
가장 작은 Value값 먼저 탐색!
1 : 1 ▶ 4
2 : 1 ▶ 2= 4번 도시 도착!

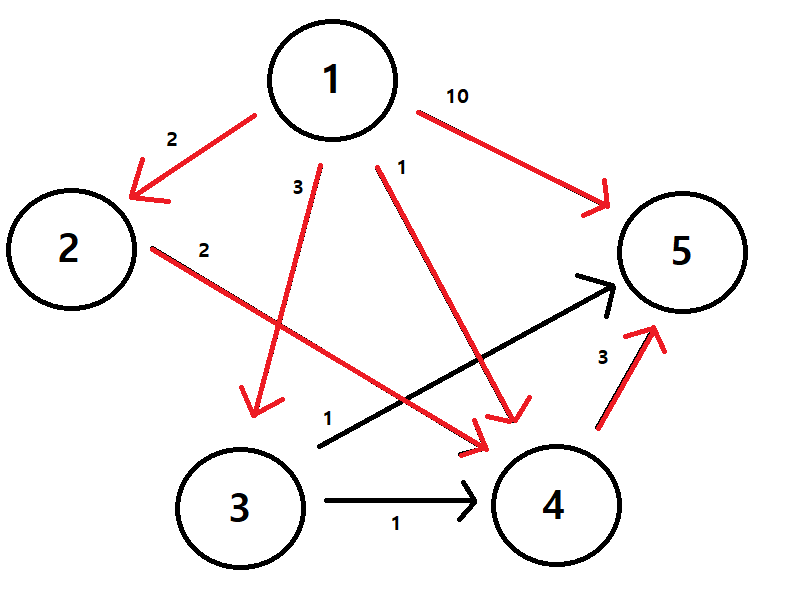
가장 작은 Value값 먼저 탐색!
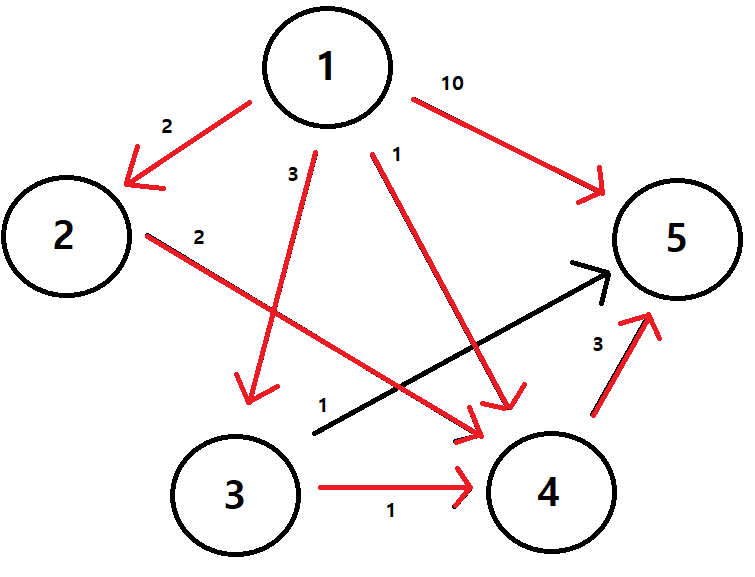
가장 작은 Value값 먼저 탐색!
3. 탐색을 통해 얻은 최소 비용을 결과를 출력합니다.
5번 최초 도착 비용 : 4
4 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 버스에 대한 정보를 띄어쓰기 기준 나누었습니다.
- 버스에 대한 정보를 ArrayList<ArrayList<>> 그래프 형태로 저장합니다.
- search함수를 진행하여 최단거리 탐색합니다.
- 최단거리를 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- search함수는 BFS에 PriorityQueue를 이용하여 최단거리를 구합니다.
결과코드
import java.io.*;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
//현재 도시 정보 및 비용 관련 클래스
static class info implements Comparable<info>{
int node, value;
public info(int node, int value){
this.node = node;
this.value = value;
}
//비용 관련 오름차순 정렬
@Override
public int compareTo(info o) {
return this.value - o.value;
}
}
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int M = Integer.parseInt(br.readLine());
StringTokenizer st;
ArrayList<ArrayList<info>> graph = new ArrayList<>();
for(int i=0;i<=N;i++)
graph.add(new ArrayList<>());
//버스에 대한 정보 그래프 형태로 저장!
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine()," ");
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int value = Integer.parseInt(st.nextToken());
graph.get(s).add(new info(e, value));
}
st = new StringTokenizer(br.readLine()," ");
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int answer = search(s, e, graph, N); //최단 거리 탐색
bw.write(answer + ""); //최단 거리 BuffredWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//BFS에서 PriorityQueue를 이용해서 최단거리 탐색 진행하는 함수
static int search(int start, int end, ArrayList<ArrayList<info>> graph, int size){
PriorityQueue<info> pq = new PriorityQueue<>();
boolean[] visited = new boolean[size+1];
pq.add(new info(start, 0)); //시작 도시 저장!
//최단 거리 탐색
while(!pq.isEmpty()){
info cur = pq.poll();
if(cur.node == end) //최초 목적 도시 도착!
return cur.value;
visited[cur.node] = true; //현재 도시 방문!
//버스 경로 탐색!
for(info next : graph.get(cur.node)){
if(!visited[next.node]) //방문하지 않았던 도시일 때
pq.add(new info(next.node, cur.value + next.value));
}
}
return -1; //해당 도시에 도달하지 못할 때
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(재귀, JAVA)2448번, 별 찍기 - 11 (0) | 2023.01.24 |
|---|---|
| [백준] 알고리즘 분류(그래프 이론,JAVA)12851번, 숨바꼭질 2 (0) | 2023.01.24 |
| [백준] 알고리즘 분류(다이나믹 프로그래밍,JAVA)2096번, 내려가기 (0) | 2023.01.23 |
| [백준] 알고리즘 분류(백트래킹,JAVA)15666번, N과 M(12) (0) | 2023.01.22 |
| [백준] 알고리즘 분류(다이나믹 프로그래밍,JAVA)9465번, 스티커 (2) | 2023.01.22 |




댓글