문제 링크
1016번: 제곱 ㄴㄴ 수
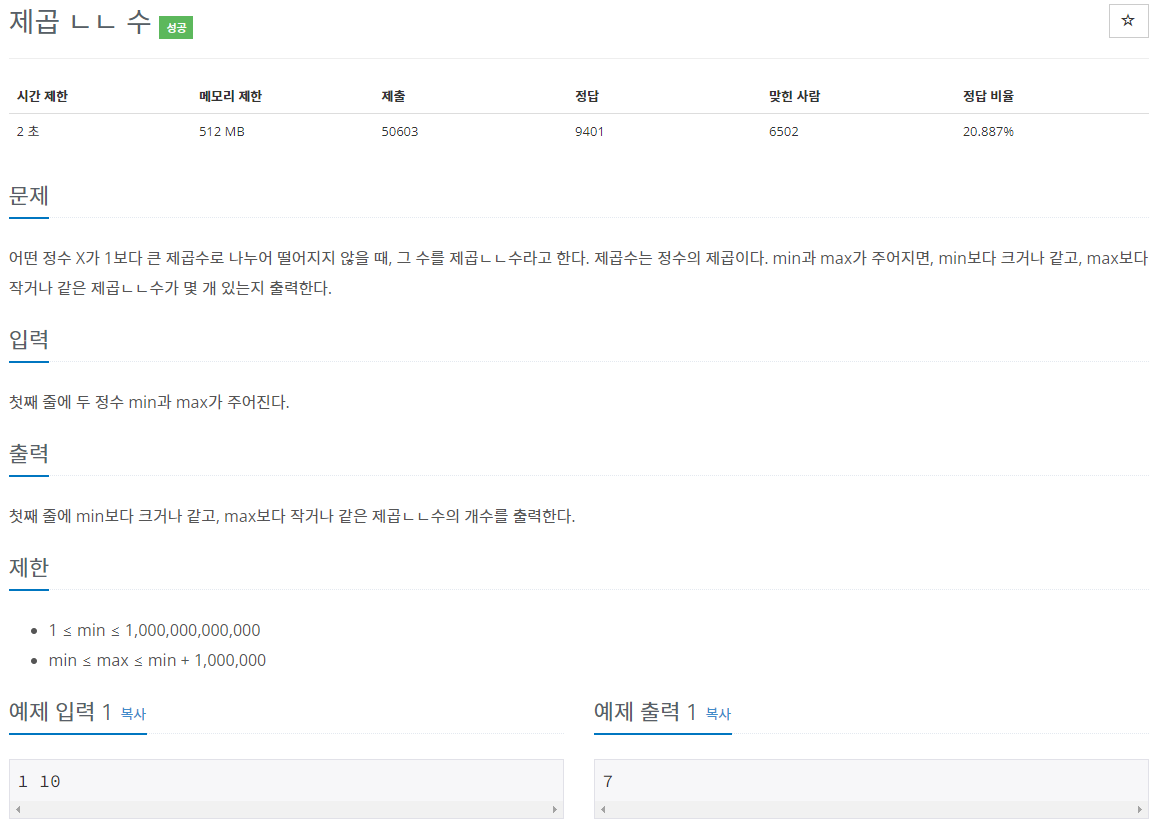
어떤 정수 X가 1보다 큰 제곱수로 나누어 떨어지지 않을 때, 그 수를 제곱ㄴㄴ수라고 한다. 제곱수는 정수의 제곱이다. min과 max가 주어지면, min보다 크거나 같고, max보다 작거나 같은 제곱ㄴㄴ수
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. A이상 B이하의 수에서 1보다 큰 제곱수로 나누어 떨어지지 않는 개수를 결과로 출력합니다.
2. A와 B의 자연수 범위는 int형을 벗어나있습니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 제곱수 기준 에라토스테네스의 체를 이용하여 탐색합니다.
3. 탐색이 끝나고 제곱수에 나누어 떨어지지 않는 값의 개수를 결과로 출력합니다.
※이 문제는 혼자 풀어보다가 도저히 아이디어가 떠오르지 않아서 다른 분들의 코드를 참고하였습니다.
제곱수 기준 탐색
min ≤ n ≤ max의 범위가 제곱수의 나누어 떨어지는지 저장하는 배열을 만들어보려고 했지만
min과 max가 int형 범위를 벗어날 수 있기에 해당 배열을 만드는 것부터 큰 고민이 있었습니다.
다른 분들의 코드에서 배열의 크기를 [max - min]의 크기만큼 설정한 뒤
해당 인덱스들이 가리키는 값들은 0 ~ max-min값이 아닌
min + 0 , min + 1 ~ min + (max-min)의 값들로 표현할 수 있는 것입니다.
※여기서 감탄!!! 이렇게 배열을 사용해도 되구나~
Arr[0] = min + 0
Arr[1] = min + 1
Arr[2] = min + 2
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 알고리즘[편집] 2부터 소수를 구하고자 하는 구간
ko.wikipedia.org
값들을 배열에 저장해두었다면 이제는 제곱수의 나누어 떨어지는지 확인을 진행합니다.
소수를 판정할 때와 동일하게 저는 에라토스테네스의 체를 이용하여 제곱수의 맞게 떨어지는지 확인하였습니다.
여기서 Arr[]에서 가리키는 값은 (min + i)이기 때문에 제곱수의 곱을 그대로 확인하면 안됩니다!!
min % 제곱수 == 0
: min이 제곱수의 나누어 떨어지기 때문에 (min ÷ 제곱수)부터 min ≤ n ≤max에 포함됩니다.
min % 제곱수 != 0: min이 제곱수의 나누어 떨어지지 않기 때문에 (min ÷ 제곱수 + 1)부터 min ≤ n ≤max에 포함됩니다.
//나누어 떨어지는지 확인!
long s = (min % temp == 0 ? min/temp : (min / temp) + 1);
//해당 몫의 값이 min보다 크거나 같은 값중 가장 작은값!!
//min보다 크거나 같은 값부터 max보다 작거나 같은 값까지 탐색!!
//(j * temp) - min : index가 가리키는 것은 min + i의 형태이기 때문에
//인덱스의 형태로 표현하기 위해서 연산을 진행!
for (long j = s; j * temp <= max; j++) {
prime[(int) (j * temp - min)] = true;
}
예제입력 1.
1. 입력된 정보를 저장합니다.
min : 1
max : 10
2. 제곱수 기준 에라토스테네스의 체를 이용하여 탐색합니다.
제곱수로 나누어 떨어지는지 확인하는 배열을 만들기 위해 크기 계산
max ≤ n ≤ min = 10 - 1 + 1 = 10개
prime[0~9] 설정!
prime[0] = min + 0 = 1
prime[1] = min + 1 = 2
prime[2] = min + 2 = 3
....
2 × 2 = 4
min % 9 = 1
3. 탐색이 끝나고 제곱수에 나누어 떨어지지 않는 값의 개수를 결과로 출력합니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| True | True | True |
10 - 3 = 7개 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 min와 max를 저장합니다.
- isPrime를 실행하여 제곱수로 나누어 떨어지는 값들을 탐색합니다.
- 탐색이 끝난 뒤 제곱수로 나누어 떨어지지 않는 값의 개수를 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- isPrime함수는 에라토스테네스의 체를 이용하여 값들이 제곱수로 나누어 떨어지는지 탐색합니다.
결과코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static boolean[] prime; // 제곱수로 나누어떨어지는지 확인하는 배열
public static void main(String[] args) throws IOException {
// 입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
// 입력값 max, min 저장
long min = Long.parseLong(st.nextToken());
long max = Long.parseLong(st.nextToken());
int size = (int) (max - min); // 제곱수 나누어떨어지는지 확인하는 범위 계산
prime = new boolean[size + 1]; // 범위에 맞게 확인 배열 크기 설정!
isPrime(min, max); // 에라토스테네스의 체를 이용한 탐색 진행!
int result = 0;
// 제곱수로 나누어 떨어지지 않는 개수를 구하기
for (int i = 0; i <= size; i++) {
if (!prime[i])
result++;
}
bw.write(String.valueOf(result)); // 개수 BufferedWriter 저장
bw.flush(); // 결과 출력
bw.close();
br.close();
}
// 에라토스테네스의 체를 이용해 제곱수로 나누어 떨어지는지 탐색하는 함수
static void isPrime(long min, long max) {
// Math.sqrt()는 나올 수 있는 최대에 제곱근까지만 탐색하도록 범위 설정!
for (long i = 2; i <= Math.sqrt(max); i++) {
long temp = i * i; // 현재 제곱수 계산
// 시작되는 몫의 최소값 구하기!
long s = (min % temp == 0 ? min / temp : (min / temp) + 1);
// 시작되는 몫부터 제곱수를 더해가며 나누어 떨어지는 값들 확인
for (long j = s; j * temp <= max; j++)
prime[(int) (j * temp - min)] = true;
}
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(다이나믹 프로그래밍,JAVA)9084번, 동전 (0) | 2023.02.25 |
|---|---|
| [백준] 알고리즘 분류(그래프 이론,JAVA)4485번, 녹색 옷 입은 애가 젤다지? (0) | 2023.02.25 |
| [백준] 알고리즘 분류(백트래킹,JAVA)6987번, 월드컵 (2) | 2023.02.21 |
| [백준] 알고리즘 분류(자료구조,JAVA)13334번, 철로 (0) | 2023.02.20 |
| [백준] 알고리즘 분류(다이나믹 프로그래밍,JAVA)1965번, 상자넣기 (0) | 2023.02.20 |




댓글