문제 링크
9084번: 동전
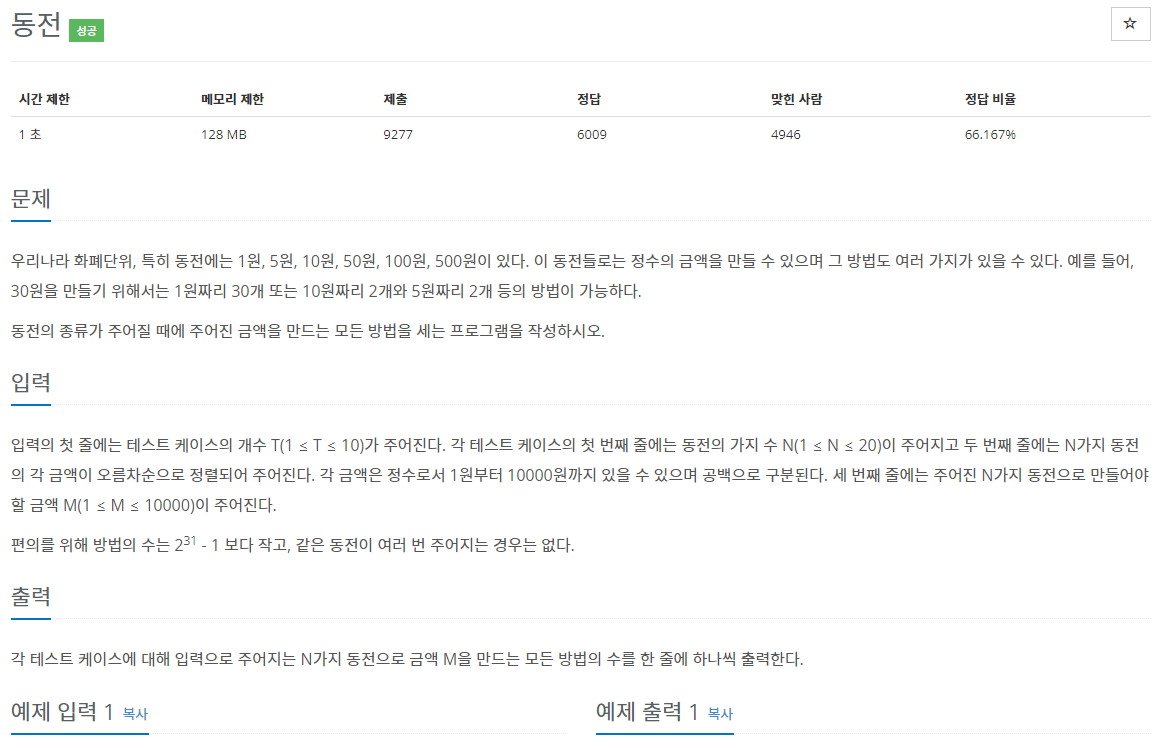
우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. 동전은 N가지가 주어지며, 동전은 마음대로 사용할 수 있습니다.
2. N개의 동전을 가지고 M을 만드는 모든 개수를 결과로 출력합니다.
3. 결과는 int형 범위 안에 존재합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 동전의 사용하는 경우에 대한 DP[][]를 구성합니다.
3. 구성이 끝나고 DP[N][M]의 값을 결과로 출력합니다.
DP 구성!
이 문제를 냅색 알고리즘과 비슷하게 DP[][]를 구성하였습니다.
Knapsack problem - Wikipedia
From Wikipedia, the free encyclopedia Problem in combinatorial optimization Example of a one-dimensional (constraint) knapsack problem: which boxes should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15
en.wikipedia.org
DP[][]를 구성할 때 가장 중요한 2가지!
DP[i][j]
i : 0 ~ i까지의 동전 사용 경우
j : 만들어야 할 금액
1. DP[0~N][0] = 1
0원은 어떤 종류의 동전이 있더라도
아무것도 사용하지 않으면 0원을 만들 수 있기 때문에 1으로 초기화할 수 있습니다.
2. 점화식
coin[i] <= j
해석 : 만들어야 하는 금액이 현재 동전의 비용보다 크거나 같을 때(현재 코인 사용 가능!)
점화식 : DP[i-coin[i]][j] + DP[i-1][j]
coin[i] > j
해석 : 만들어야 하는 금액이 현재 동전의 비용보다 작을 때(현재 코인 사용 불가능!)
점화식 : DP[i-1][j]
DP[i-1][j] : 0 ~ (i-1)까지의 동전을 사용해서 j을 만드는 모든 경우의 개수 : 현재 동전 사용 X
DP[i-coin[i][j] : 0 ~(i-coin[i])까지의 동전을 사용해서 j을 만드는 모든 경우의 개수 : 현재 동전 사용 O
DP[i-coin[i]][j] + DP[i-1][j] : 현재 동전 사용하지 않는 경우와 사용한 경우를 더하는 것입니다.
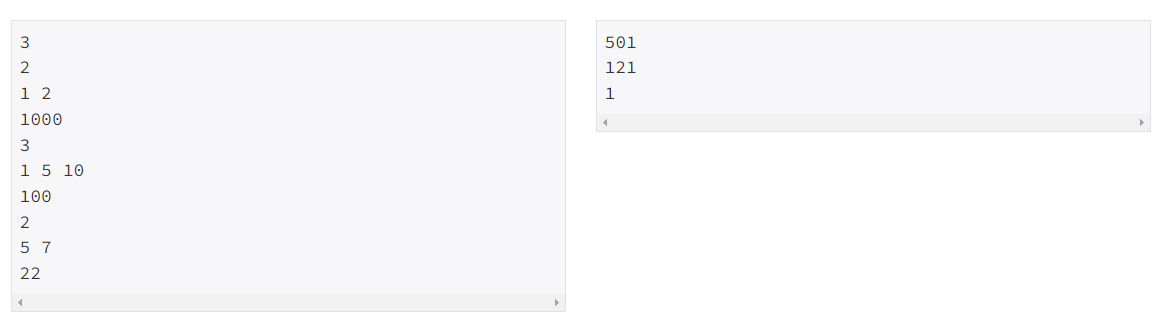
예제입력 1.
1. 입력된 정보를 저장합니다.
※3번째 테스트케이스가 진행되는 과정만 설명하도록 하겠습니다.
N : 2
2. 동전의 사용하는 경우에 대한 DP[][]를 구성합니다.
기본 DP[][] 테이블 구성
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | .... | 20 | 21 | 22 | ||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1(5) | 1 | ||||||||||||||||||
| 2(7) | 1 | ||||||||||||||||||
1번 코인(5) 탐색!
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | .... | 20 | 21 | 22 | ||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 1(5) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 2(7) | 1 | ||||||||||||||||||
....
DP[1][4] = DP[i-1][0] = DP[0][4] = 0DP[1][5] = DP[i][j-5] + DP[i-1][j] = DP[1][0] + DP[0][5] = 1 + 0 = 1DP[1][6] = DP[i][j-5] + DP[i-1][j] = DP[1][1] + DP[0][6] = 0 + 0 = 0
....
2번 코인(7) 탐색!
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | .... | 20 | 21 | 22 | ||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 1(5) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 2(7) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 1 | 1 | 1 | |
....
DP[2][5] = DP[i-1][0] = DP[1][5] = 1
DP[2][6] = DP[i-1][0] = DP[1][6] = 0
DP[2][7] = DP[i][j-7] + DP[i-1][j] = DP[2][0] + DP[1][7] = 1 + 0 = 1
....
3. 탐색이 끝나고 DP[]의 최대 값을 결과로 출력합니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | .... | 20 | 21 | 22 | ||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 1(5) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | |
| 2(7) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ... | 1 | 1 | 1 | |
DP[2][22] = 1개 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 동전의 종류를 띄어쓰기 기준 나누었습니다.
- 점화식을 이용하여 DP[][] 테이블을 구성합니다.
- DP[N][M]의 값을 결과로 BufferedWriter에 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
결과코드
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int[] coin; //동전의 종류
static int[][] DP; //동전 경우 저장할 메모이제이션
static int N, M;
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
StringTokenizer st;
//각 테스트케이스 진행
for(int tc = 1; tc <= T; tc++){
N = Integer.parseInt(br.readLine());
coin = new int[N+1];
st = new StringTokenizer(br.readLine()," ");
//코인 종류 저장
for(int i=1;i<=N;i++)
coin[i] = Integer.parseInt(st.nextToken());
M = Integer.parseInt(br.readLine());
DP = new int[N+1][M+1];
//0원은 무조건 1개 만들 수 있습니다.(동전 0개 사용)
for(int i=0;i<=N;i++)
DP[i][0] = 1;
//점화식을 이용한 DP[][] 구성
for(int i=1;i<=N;i++){
int value = coin[i];
for(int j=1;j<=M;j++){
DP[i][j] = DP[i-1][j];
if(j >= value)
DP[i][j] += DP[i][j - value];
}
}
bw.write(String.valueOf(DP[N][M])); //결과 BufferedWriter 저장
bw.newLine();
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(누적합,JAVA)17305번, 사탕 배달 (0) | 2023.03.10 |
|---|---|
| [백준] 알고리즘 분류(그래프 이론,JAVA)9205번, 맥주 마시면서 걸어가기 (0) | 2023.03.09 |
| [백준] 알고리즘 분류(그래프 이론,JAVA)4485번, 녹색 옷 입은 애가 젤다지? (0) | 2023.02.25 |
| [백준] 알고리즘 분류(수학,JAVA)1016번, 제곱 ㄴㄴ 수 (0) | 2023.02.22 |
| [백준] 알고리즘 분류(백트래킹,JAVA)6987번, 월드컵 (2) | 2023.02.21 |




댓글