문제 링크
11973번: Angry Cows (Silver)
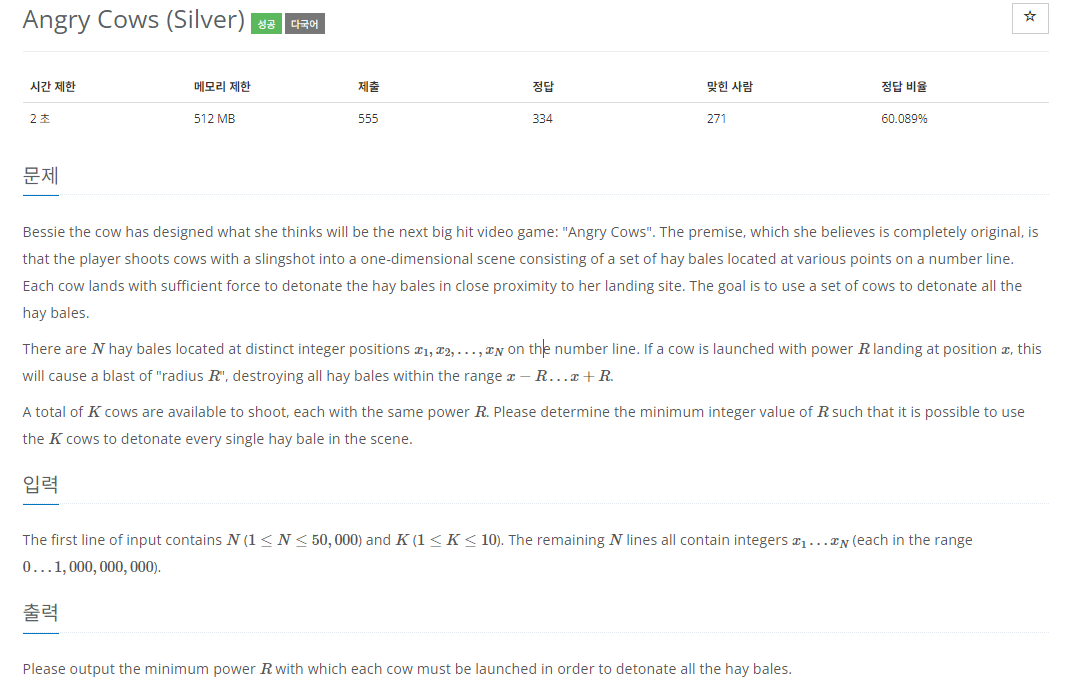
The first line of input contains \(N\) (\(1 \leq N \leq 50,000\)) and \(K\) (\(1 \leq K \leq 10\)). The remaining \(N\) lines all contain integers \(x_1 \ldots x_N\) (each in the range \(0 \ldots 1,000,000,000\)).
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
접근 방법
이 문제에 핵심
1. N개의 건초가 존재하며, K개의 소가 존재합니다.
2. K개의 소가 배치되면 ± R 범위의 건초들이 사라집니다.
3. 모든 건초를 제거하는 R의 최소값을 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 이분탐색을 통해 R의 최소값을 탐색합니다.
3. 최소값으로 얻은 R의 값을 결과로 출력합니다.
이분 탐색
R으로 나올 수 있는 수는 0 ~ 1,000,000,000 사이의 값이 존재합니다.
하지만, 항상 1,000,000,000의 값이 포함되는 것은 아니기 때문에 입력되는 건초의 위치 최대값을 기준으로 이분탐색을 진행합니다.
0 ~ 건초의 최대 위치값
Start : 0
End : 건초의 최대 위치값
소를 놓는 최상의 위치는
현재 터지지 않는 건초값 + R이 됩니다.
| 현재 최소 건초 위치 | + R | + R × 2 |
이분 탐색을 진행하면서, 구분하는 조건
1. 마지막에 터진 소가 없애는 범위가 건초의 최대 위치보다 크거나 같을 때
→ end = mid
2. 마지막에 터진 소가 없애는 범위가 건초의 최대 위치보다 작을 때
→ start = mid + 1
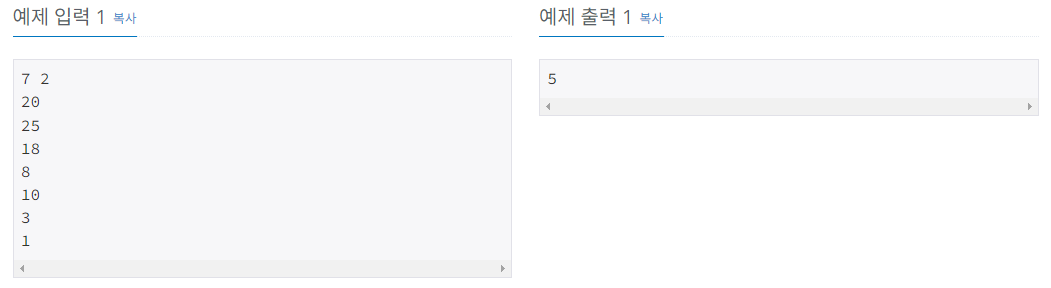
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 7
K : 2
건초 위치
최대값 : 25
| 20 | 25 | 18 | 8 | 10 | 3 | 1 |
2. 이분탐색을 통해 R의 최소값을 탐색합니다.
건초 위치를 오름차순 정렬합니다.
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
이분 탐색을 진행합니다.
Start : 0
End : 건초 최대값(25)
mid = (0 + 25) / 2 = 12
소 배치
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(1) + 12 = 13 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | X | X | X |
건초 제거 범위 : 1 ≤ 소(13) ≤ 25
조건의 만족!
→ end = mid(12)
Start : 0
End : 12
mid = (0 + 12) / 2 = 6
소 배치
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(1) + 6 = 7 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | O | O | O |
건초 제거 범위 : 1 ≤ 소(8) ≤ 15
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(18) + 6 = 24 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | X | X | X |
건초 제거 범위 : 18 ≤ 소(24) ≤ 30
조건의 만족!
→ end = mid(6)
Start : 0
End : 6
mid = (0 + 6) / 2 = 3
소 배치
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(1) + 3 = 4 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | O | O | O | O | O |
건초 제거 범위 : 1 ≤ 소(4) ≤ 7
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(8) + 3 = 11 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | O | O | O |
건초 제거 범위 : 8 ≤ 소(11) ≤ 14
조건의 불만족!
→ start = mid(3) + 1 = 4
Start : 4
End : 6
mid = (4 + 6) / 2 = 5
소 배치
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(1) + 5 = 6 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | O | O | O |
건초 제거 범위 : 1 ≤ 소(6) ≤ 11
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(18) + 5 = 23 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | X | X | X |
건초 제거 범위 : 18 ≤ 소(23) ≤ 28
조건의 만족!
→ end = mid(5)
Start : 4
End : 5
mid = (4 + 5) / 2 = 4
소 배치
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(1) + 4 = 5 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | O | O | O | O |
건초 제거 범위 : 1 ≤ 소(5) ≤ 9
현재 건초 최소값 기준 +R 위치에 소 배치 : 최소값(10) + 4 = 14 위치에 배치
| 1 | 3 | 8 | 10 | 18 | 20 | 25 |
| X | X | X | X | X | O | O |
건초 제거 범위 : 10 ≤ 소(14) ≤ 18
조건의 만족!
→ start = mid(4) + 1 = 5
start(5) == end(5)으로써
탐색을 종료합니다.
3. 최소값으로 얻은 R의 값을 결과로 출력합니다.
이분 탐색으로 얻은 R의 최소값 5을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 N과 K를 띄어쓰기 기준 나누었습니다.
- 건초의 최대 위치를 이용한 이분 탐색을 진행합니다.
- 이분탐색의 조건은 소를 배치하는 최상의 경우에서 모든 건초를 먹는지 확인하며 진행합니다.
- 탐색이 끝난 뒤 R의 최소값을 결과로 BufferedWriter 저장합니다.
- BufferedWriter에 저장된 결과를 출력합니다.
결과코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//입력값 저장
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int max = 0;
int[] dummy = new int[N];
for(int i=0;i<N;i++){
dummy[i] = Integer.parseInt(br.readLine());
//최대 건초 위치 구하기
max = Math.max(max,dummy[i]);
}
//건초 위치 기준 오름차순 정렬
Arrays.sort(dummy);
int start = 0;
int end = max;
int mid;
//이분 탐색 진행
while(start < end){
//중간값
mid = (start+end)/2;
//초기 건초 최소값 기준 소의 커버 범위
long cur = dummy[0] + mid * 2L;
int cnt = 1;
//소가 건초를 없애는 최상의 경우 진행
for(int i=1;i<N;i++){
if(cur >= dummy[i]){
continue;
}
if(cnt == K){
break;
}
cur = dummy[i] + mid * 2;
cnt++;
}
//소가 건초를 모두 먹을 때 조건 달성!
if(cur >= dummy[N-1]) {
end = mid;
}else{ //소가 건초를 모두 먹지 못할 때 조건 미달성...
start = mid + 1;
}
}
//이분탐색으로 얻은 최소 R의 값 BufferedWriter 저장
bw.write(String.valueOf(start));
bw.flush(); //결과 출력
bw.close();
br.close();
}
}'백준' 카테고리의 다른 글
| [백준, Java] 16562번, 친구비(BFS) (0) | 2023.11.05 |
|---|---|
| [백준, Java] 1939번, 중량제한(다익스트라) (2) | 2023.11.03 |
| [백준, Java] 1441번, 나누어 질까(정수론) (2) | 2023.10.29 |
| [백준, Java] 3142번, 즐거운 삶을 위한 노력(정수론) (2) | 2023.10.26 |
| [백준, Java] 12944번, 재미있는 숫자 놀이(정수론) (0) | 2023.10.24 |




댓글