주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명
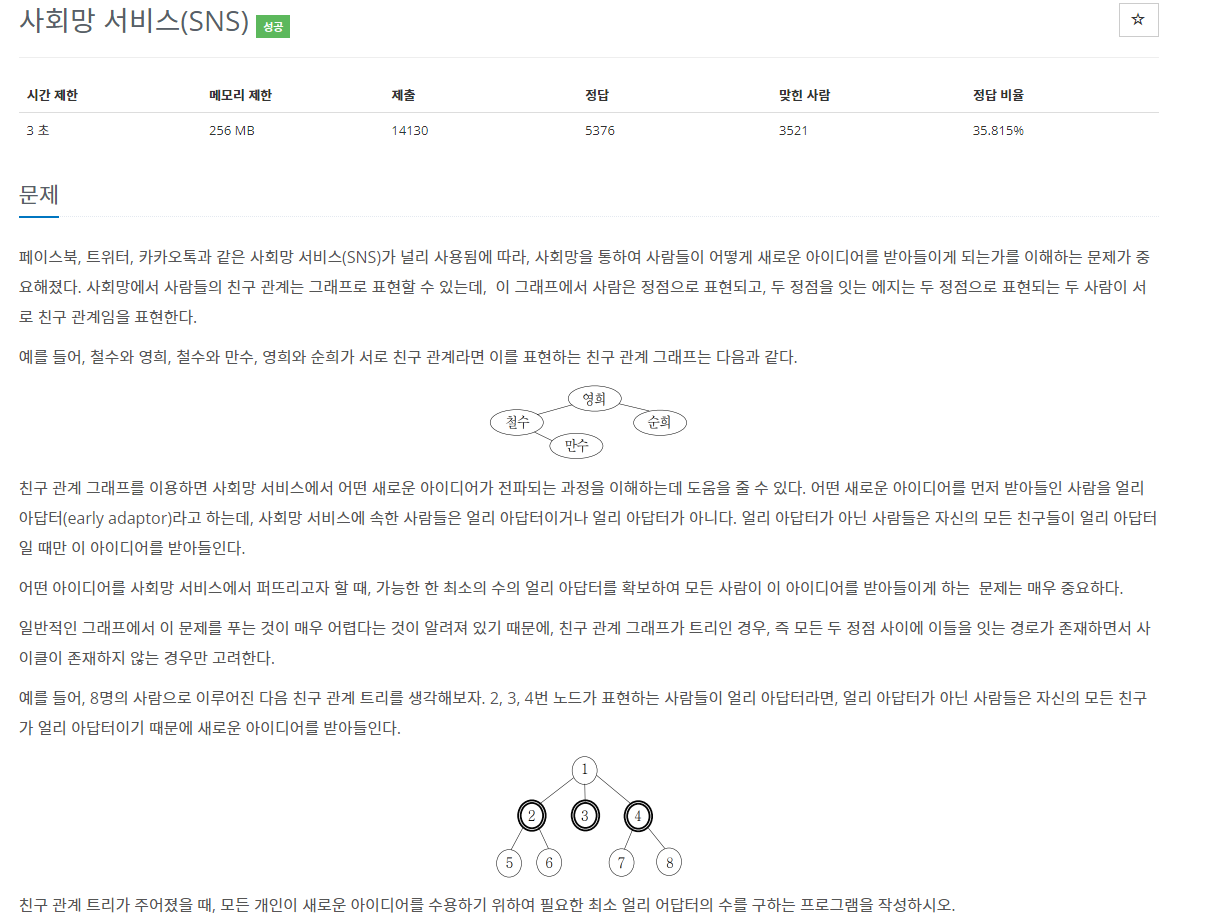

접근 방법
트리
서로 다른 두 노드를 잇는 길이 하나뿐인 그래프(사이클 X)
트리 구조 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
동적계획법
동일한 연산을 계속 반복하여 비효율적으로 코드가 실행되어 그것을 향상시키기 위하여 반복되는 연산의 결과를 따로 저장하여 적재적소에 코드가 더 효율적으로 만드는 방법입니다.
이 문제에 핵심은
1. 그래프에 대한 정보가 주어집니다.
2. 인접한 모든 정점이 얼리 어답터이면 자신도 새로운 아이디어를 받아들인다.
3. 모든 친구가 새로운 아이디어를 받아들이는 최소 얼리 어답터의 수를 결과로 출력한다.
입력받은 그래프 내용에 대해서 트리의 형태로 만들어주었습니다.
※저는 루트 노드를 1로 설정하고 트리를 만들었습니다.
DFS탐색으로 모든 친구가 새로운 아이디어를 받아들이는 모든 경우를 만들었습니다.
DFS 탐색을 진행할 때 2가지로 나뉠 수 있습니다.
현재 탐색하는 친구가 얼리 어답터일 때 : 인접한 친구들은 얼리 어답터이거나 아니어도 된다.
현재 탐색하는 친구가 얼리 어답터가 아닐 때 : 인접한 친구들은 무조건 얼리 어답터이어야 한다.
위 과정을 탐색할 때 메모이제이션을 이용하여 반복되는 연산을 최소화하였습니다.
메모이제이션의 값을 이용하여 최소 얼리 어답터의 수를 구하였습니다.
예제입력1
그래프의 값을 트리의 형태로 만들기
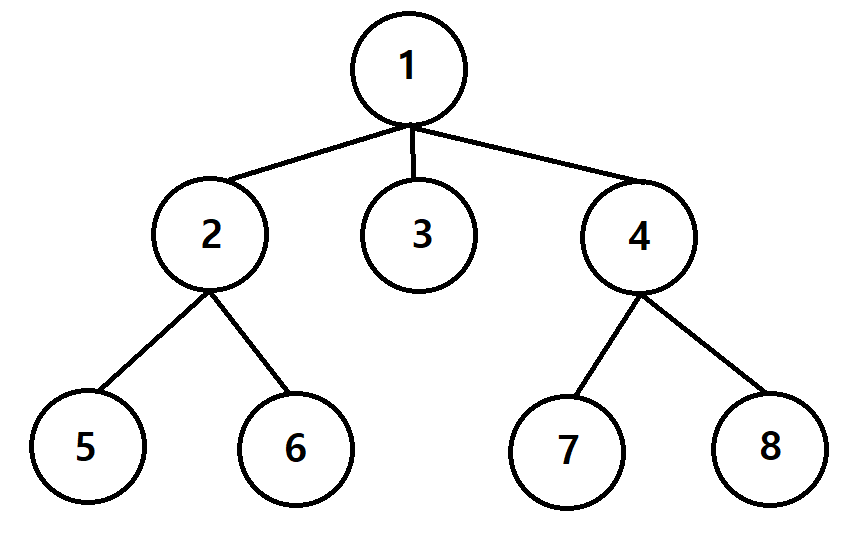
루트 정점 1이 얼리 어답터일 때 : 정점 2, 3, 4는 얼리 어답터이거나 아니어도 된다.
정점 2을 얼리 어답터일 때 : 정점 5,6은 얼리 어답터이거나 아니어도 된다.
정점 2가 얼리 어답터가 아닐 때 : 정점 5, 6은 얼리 어답터이어야 한다.
.....
위 과정을 DFS로 진행하면 최소 얼리어답터의 경우를 구할 수 있습니다.

최소 얼리 어답터의 수 : 3
- BufferedReader를 사용하여 입력 값을 저장하였습니다.
- StringTokenizer를 사용하여 그래프에 대한 정보를 저장합니다.
- 루트 정점 1로 하는 트리를 만드는 buildTree함수를 실행하였습니다.
- DFS와 메모이제이션을 이용하여 루트 정점에 따른 최소 얼리 어답터 수를 구하는 search함수를 실행하였습니다.
- BufferedWriter에 최소 얼리 어답터 수를 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- buildTree함수는 주어진 그래프를 트리의 형태로 만드는 함수입니다.
- search함수는 DFS와 메모이제이션을 이용하여 얼리 어답터가 만들어지는 모든 경우에 최소값을 만듭니다.
결과 코드
import java.util.*;
import java.io.*;
public class Main {
static int N;
static ArrayList<ArrayList<Integer>> graph = new ArrayList<>(); //그래프 저장 리스트
static ArrayList<ArrayList<Integer>> tree = new ArrayList<>(); //트리 저장 리스트
static int[][] DP; //메모이제이션 배열
static public void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//입력값 처리하는 BufferedReader
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//결과값 출력하는 BufferedWriter
StringTokenizer st;
N = Integer.parseInt(br.readLine());
DP = new int[N+1][2];
for(int i=0;i<=N;i++){
graph.add(new ArrayList<>());
tree.add(new ArrayList<>());
}
//입력되는 그래프 값 저장
for(int i=0;i<N-1;i++){
st = new StringTokenizer(br.readLine()," ");
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
graph.get(u).add(v);
graph.get(v).add(u);
}
buildTree(1, 0); //루트 정점 1 기준으로 트리 만들기
int rootInclude = search(1, 1); //루트 정점 1이 얼리 어답터일 때
int rootNonInclude = search(1, 0); //루트 정점1이 얼리 어답터가 아닐 때
if(rootInclude<rootNonInclude) //루트 정점 얼리 어답터 유무로 비교
bw.write(rootInclude + "\n");
else
bw.write(rootNonInclude + "\n");
bw.flush(); //결과 출력
bw.close();
br.close();
}
//DFS탐색으로 모든 친구가 새로운 아이디어를 받아들이는 경우를 구하는 함수
static int search(int cur, int check) {
if (DP[cur][check] != 0) //이미 연산해본 경우
return DP[cur][check];
int result = 0;
if (check == 1) { //현재 정점이 얼리 어답터일 경우
result +=1 ;
for (Integer next : tree.get(cur)) {
int include = search(next, 0); //인접한 친구가 얼리 어답터가 아닐 때
int nonInclude = search(next, 1); //인접한 친구가 얼리 어답터일 때
if(include<nonInclude)
result += include;
else
result += nonInclude;
}
} else { //현재 정점이 얼리 어답터가 아닌 경우
for(Integer next : tree.get(cur)){
result += search(next, 1); //인접한 친구가 얼리 어답터일 때
}
}
return DP[cur][check] = result;
}
//그래프 형태를 트리 형태로 바꾸는 함수
static void buildTree(int cur, int parent){
for(Integer next : graph.get(cur)){
if(next!=parent){
tree.get(cur).add(next);
buildTree(next, cur);
}
}
}
}'백준' 카테고리의 다른 글
| [백준] code.plus(BFS 알고리즘,JAVA)12886번, 돌 그룹 (0) | 2022.06.21 |
|---|---|
| [백준] 단계별로 풀어보기(단계:32, 트리에서의 동적 계획법,JAVA)1949번, 우수 마을 (0) | 2022.06.20 |
| [백준] code.plus(BFS 알고리즘,JAVA)14502번, 연구소 (0) | 2022.06.18 |
| [백준] 단계별로 풀어보기(단계:32, 트리에서의 동적 계획법,JAVA)2213번, 트리의 독립집합 (0) | 2022.06.17 |
| [백준] code.plus(BFS 알고리즘,JAVA)16948번, 데스 나이트 (0) | 2022.06.17 |




댓글