문제 링크
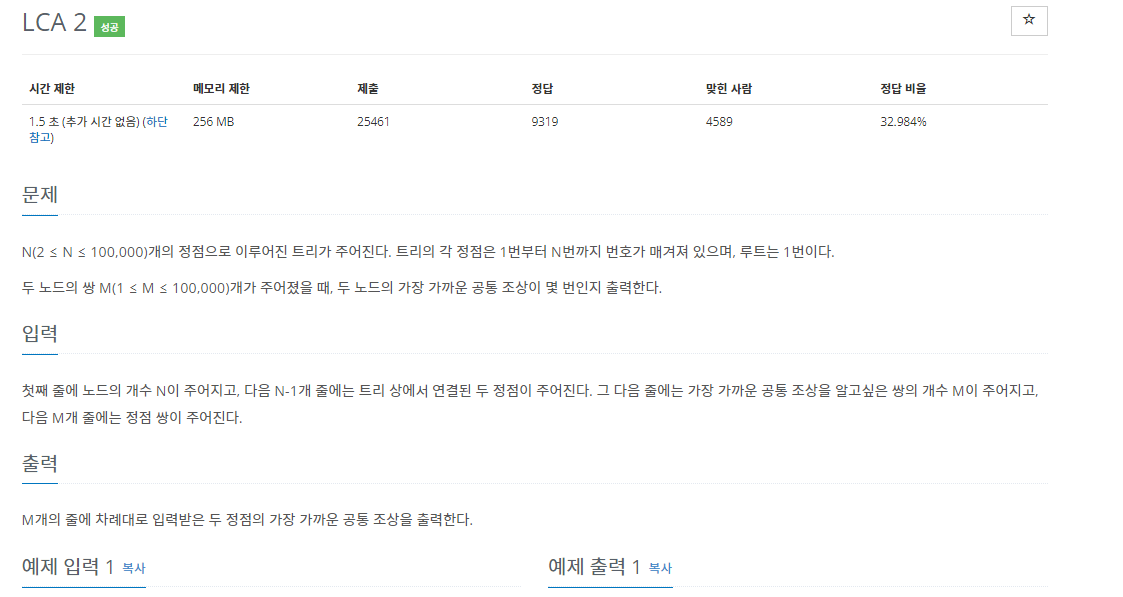
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
이 문제에 핵심
1. 트리에 대한 정보가 주어지고 두 노드의 가장 가까운 공통 조상 노드를 결과로 출력합니다.
2. 루트 노드는 항상 1번입니다.
3. 트리의 각 정점은 1번~N번까지 존재합니다.
이 문제를 풀기 전 LCA에 대한 문제가 처음이라면 먼저 풀고 오시는 것을 추천드립니다.
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
[백준] 알고리즘 분류(트리,JAVA)11437번, LCA
문제 링크 11437번: LCA 첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고
tussle.tistory.com
위 링크의 문제와 이 문제의 차이점이라면 입력되는 트리의 양이 10,000 → 100,000으로 변경되어서 원래 코드대로 진행하면 시간 초과가 발생합니다.
진행되는 과정은 비슷하지만 이분 탐색과 DP를 사용하여 조상 노드를 찾는 과정의 시간 복잡도를 줄이는 방향으로 설계되었습니다.
알고리즘 진행 순서.
1. 입력된 트리의 정보를 저장합니다.
2. 입력된 정보로 트리 형성 및 부모 노드(DP)와 깊이를 따로 저장합니다.
3. M개의 노드 쌍에 대한 공통 조상 노드를 찾아서 결과로 출력합니다.
DP 구성하기
조상노드에 대하여 메모이제이션인 parent[][]를 구성하였습니다.
parent[m][n] = m번 노드의 2ⁿ만큼 위에 있는 부모 노드를 가리키도록 됩니다.
parent[3][1] = 3번 노드의 2¹(2)만큼 위에 있는 부모 노드를 표현
parent[5][2] = 5번 노드의 2²(4)만큼 위에 있는 부모 노드를 표현

위 그림을 살펴보면 2번 노드는 Parent[9][1]이기도 하지만 Parent[4][0]이기도 합니다.
다른 예로는 1번 노드는 Parent[15][2]이기도 하지만 Parent[5][1], Parent[2][0]이기도 합니다.
이 과정을 통해서 Parent[][]의 값을 구하는 점화식을 구하실 수 있습니다.
Parent[m][n] = Parent[Parent[m][n-1]][n-1]
위 점화식을 이용하면 모든 Parent[][]를 구성하실 수 있습니다.
공통 조상 노드 구하기
※11437번 LCA와 과정은 동일하지만 DP를 사용한다는 차이점만 존재합니다.
1. 두 노드의 깊이가 다르면 같도록 바꾼다.
깊이가 같아지도록 바꿀 때에도 이진 탐색을 이용해서 탐색하는 횟수를 줄이도록 진행하였습니다.

2. 깊이가 같아지면 부모 노드로 동시에 이동하며 같은 노드를 가리킬 때까지 반복합니다.
깊이가 같아질 때에도 깊이를 1씩 올리는 것이 아닌 이분탐색으로 탐색하여 같은 노드가 가리킬 때까지 반복합니다.

3. 이분 탐색이 종료되었을 때 가리키는 부모 노드를 결과로 출력합니다.
부모 노드 : 1번 노드
예제입력 1.
1. 입력된 트리의 정보를 저장합니다.
N : 15
노드 연결 쌍 : (1, 2), (1, 3), (2, 4), (3, 7), (6, 2), (3, 8), (4, 9), (2, 5), (5, 11), (7, 13), (10, 4), (11, 15), (12, 5), (14, 7)
M : 6
최소 공통 조상 노드 찾아야 할 쌍 : (6, 11), (10, 9), (2, 6), (7, 6), (8, 13), (8, 15)
2. 입력된 정보로 트리 형성 및 부모 노드(DP)와 깊이를 따로 저장합니다.

부모 노드의 parent[m][0](1칸 위에 있는 부모 노드)를 저장하였습니다.
parent[15][0] = 11, parent[2][0] = 1
.....
노드의 깊이도 배열로 따로 저장하였습니다.
depth[15] = 5, depth[2] = 2
.....
점화식을 이용하여 parent[][]를 구성합니다.
parent[9][1] = parent[parent[9][0]][0] = parent[4][0] = 2
parent[9][2] = parent[parent[9][1]][1] = parent[2][1] = 0(루트 노드 위에 값을 표현)
parent[15][1] = parent[parent[15][0][0] = parent[11][0] = 5
parent[15][2] = parent[parent[15][1][1] = parent[5][1] = 1
....
3. M개의 노드 쌍에 대한 공통 조상 노드를 찾아서 결과로 출력합니다.
※1번째 노드의 쌍만 공통 조상 노드를 구하는 과정을 보여드리겠습니다.
(6, 11)
최대 깊이 : 5
1) 두 노드의 깊이가 다르면 같도록 바꾼다.
depth[6] = 3
depth[11] = 4
다르기 때문에 깊이가 큰 11의 노드를 같아지도록 진행합니다.
depth[11] - depth[6] = 4 - 3 = 1로 두 깊이의 차이가 1입니다.
2⁴ = 16만큼 올라가도 같아지도록 못합니다.
2³ = 8만큼 올라가도 같아지도록 못합니다.
2² = 4만큼 올라가도 같아지도록 못합니다.
2¹ = 2만큼 올라가도 같아지도록 못합니다.
1(2의 0승) = 1만큼 올라가면 같아집니다.
11 → parent[11][0] = 5

2) 깊이가 같아지면 부모 노드로 동시에 이동하며 같은 노드를 가리킬 때까지 반복합니다.
※해당 2ⁿ 높이 만큼 올라갔을 때 같으면 현재 노드 쌍은 parent[노드 번호][n]의 변화는 필요가 없습니다.
2⁴ = 16만큼 올라가면 parent[5][4](0) == parent[6][4](0)
2³ = 8만큼 올라가면 parent[5][3](0) == parent[6][3](0)
2² = 4만큼 올라가면 parent[5][2](0) == parent[6][2](0)
2¹ = 2만큼 올라가면 parent[5][1](0) == parent[6][1](0)
1(2의 0승) = 1만큼 올라가면 parent[5][0] == parent[6][0]
3. 이분 탐색이 종료되었을 때 가리키는 부모 노드를 결과로 출력합니다.
parent[5][0] : 2를 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 통해서 노드의 관계를 띄어쓰기 기준 나누었습니다.
- 노드 간 관계를 저장한 뒤 부모 노드, 깊이 및 트리를 형성하는 setTree함수를 실행하였습니다.
- 점화식을 이용하여 부모 노드에 대한 DP를 구성하는 parentInit() 실행합니다.
- M개의 노드 쌍에 대한 LCA함수를 실행하여 최소 공통 조상 노드를 BufferedWriter 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- setTree함수는 각 노드의 관계를 이용해서 부모 노드, 깊이 및 트리를 형성하는 재귀 함수입니다.
- parentInit함수는 점화식을 이용하여 parent[][] 배열을 구성합니다.
- LCA함수는 각 노드의 깊이와 부모 노드를 이용해서 이분 탐색하여 최소 공통 조상 노드를 구하는 함수입니다.
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static ArrayList<ArrayList<Integer>> tree = new ArrayList<>(); //트리 정보 리스트
static int[] depth; //깊이 저장 배열
static int[][] parent; //부모 노드 저장 DP
static int height = 0, N;
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
//최대 높이 구하기
for(int i=1;i<=N;i*=2)
height++;
parent = new int[N+1][height];
depth = new int[N+1];
for(int i=0;i<=N;i++)
tree.add(new ArrayList<>());
//트리 정보 저장하기
for(int i=1;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
tree.get(a).add(b);
tree.get(b).add(a);
}
setTree(1, 1, 0); //트리 형태 구성 및 높이 설정
parentInit(); //점화식을 통해 부모 노드 DP 구성
int M = Integer.parseInt(br.readLine());
//M개를 LCA진행
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
bw.write(LCA(a, b) + "\n"); //LCA결과 BufferedWriter 저장
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//트리의 형태를 만드는 재귀 함수
static void setTree(int c, int d, int p){
depth[c] = d; //깊이 저장
parent[c][0] = p; //부모 노드 저장
//자식 노드들 탐색!
for(int next : tree.get(c)){
if(next == p)
continue;
setTree(next, d+1, c);
}
}
//부모 노드에 대한 DP 점화식을 이용하여 구성하는 함수
static void parentInit(){
for(int i=1;i<height;i++){
for(int j=1;j<=N;j++){
parent[j][i] = parent[parent[j][i-1]][i-1];
}
}
}
//이분탐색을 이용하여 LCA를 진행하는 함수
static int LCA(int a, int b) {
int ah = depth[a];
int bh = depth[b];
//ah가 항상 크다고 설정!
if (ah < bh) {
int temp = b;
b = a;
a = temp;
}
//높이 동일하게 맞추기
for (int i = height-1; i >= 0; i--) {
//depth[a] - depth[b]는 깊이의 차
//깊이의 차만큼 이동
if (Math.pow(2, i) <= depth[a] - depth[b])
a = parent[a][i];
}
//a와 b가 같다면 이미 공통 조상 노드에 도착했다고 판단
if(a == b)
return a;
//동시에 거슬러 올라가기
for (int i = height-1; i >= 0; i--) {
if (parent[a][i] != parent[b][i]) {
a = parent[a][i];
b = parent[b][i];
}
}
return parent[a][0];
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(트리,JAVA)2250번, 트리의 높이와 너비 (0) | 2022.10.02 |
|---|---|
| [백준] 알고리즘 분류(문자열,JAVA)9086번, 문자열 (0) | 2022.10.01 |
| [백준] 알고리즘 분류(문자열,JAVA)1357번, 뒤집힌 덧셈 (0) | 2022.09.28 |
| [백준] 알고리즘 분류(트리,JAVA)11437번, LCA (0) | 2022.09.27 |
| [백준] 알고리즘 분류(트리,JAVA)5052번, 전화번호 목록 (0) | 2022.09.26 |




댓글