문제 링크
2250번: 트리의 높이와 너비
첫째 줄에 노드의 개수를 나타내는 정수 N(1 ≤ N ≤ 10,000)이 주어진다. 다음 N개의 줄에는 각 줄마다 노드 번호와 해당 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 번호가 순서대로 주어진다.
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

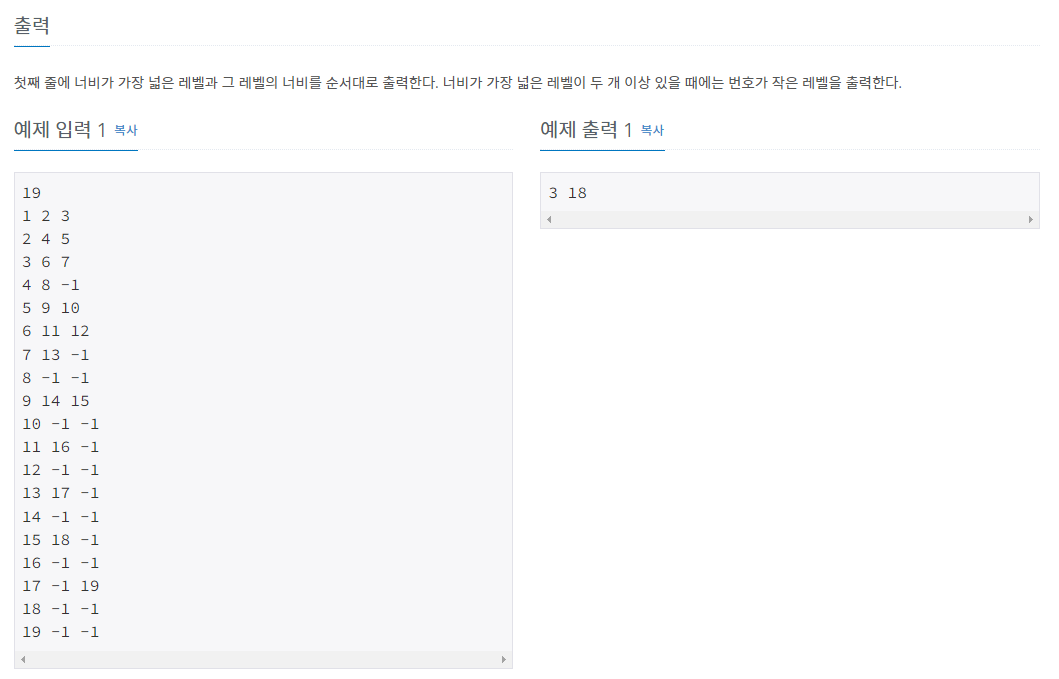
접근 방법
이 문제에 핵심
1. 트리에 대한 정보가 주어지고 각 높이의 가장 넓은 레벨과 너비를 결과로 출력합니다.
2. 루트 노드는 항상 1번은 아닙니다.
3. 자식 노드가 없는 경우 -1로 주어집니다.
4. 주어지는 트리는 이진트리입니다.
알고리즘 진행 순서.
1. 입력된 트리의 정보를 저장합니다.
2. 중위 순회를 진행하면서 각 깊이의 최소 값과 최대 값을 구합니다.
3. 각 깊이의 너비의 최대 값과 레벨을 결과로 출력합니다.
중위 순회
문제에서 표시한 그림을 살펴보면 트리를 중위 순회로 탐색하였을 때 x의 값이 정해집니다.
중위 순회는 Left → Root → Right순으로 탐색하는 방법입니다.
트리 순회 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 전산학에서 트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다. 이는 노드를 방문하는 순서에
ko.wikipedia.org

트리 중위 순회를 진행하면(4 → 2 → 5 → 1 → 3)
예제입력 1.
1. 입력된 트리의 정보를 저장합니다.
N : 19
1번 노드 : 2(left), 3(right)
2번 노드 : 4(left), 5(right)
3번 노드 : 6(left), 7(right)
4번 노드 : 8(left), -1(right)
..
19번 노드 : -1(left), -1(right)
트리에 대한 그림은 문제에서 보여주고 있으므로 생략하겠습니다.
2. 중위 순회를 진행하면서 각 깊이의 최소 값과 최대 값을 구합니다.
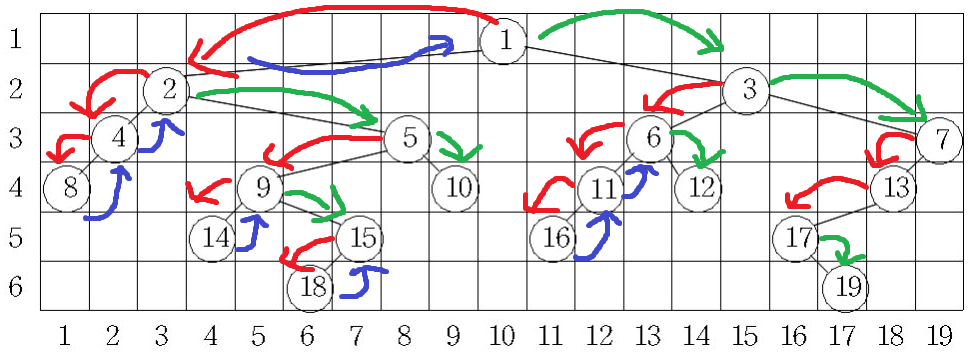
중위 순회 진행(Left → Root → Right)
8 → 4 → 2 → 14 → 9 → 18 → 15 → 5 → 10 → 1 → 16 → 11 → 6 → 12 → 3 → 19 → 17 → 13 → 7
8 : 1
4 : 2
2 : 3
...
7 : 19
깊이 1 : 최대 10(1), 최소 10(1)
깊이 2 : 최대 15(3), 최소 3(2)
깊이 3 : 최대 19(7), 최소 2(4)
깊이 4 : 최대 18(13), 최소 1(8)
깊이 5 : 최대 16(17), 최소 4(14)
깊이 6 : 최대 17(19), 최소 6(18)
3. 각 깊이의 너비의 최대 값과 레벨을 결과로 출력합니다.
※ +1을 하는 이유는 너비의 범위가 min ≤ n ≤ max이므로 범위를 구할 때 max - min + 1입니다.
깊이 1 = 10 - 10 + 1 = 1
깊이 2 = 15 - 3 + 1= 13
깊이 3 = 19 - 2 + 1= 18
깊이 4 = 18 - 1 + 1 = 18
깊이 5 = 16 - 4 + 1 = 13
깊이 6 = 17 - 6 + 1 = 12
깊이 3과 너비 18을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 통해서 트리의 정보를 띄어쓰기 기준 나누었습니다.
- 중위 순회를 하는 dfs함수를 실행하였습니다.
- 각 깊이 중 최대 너비와 그에 해당하는 깊이를 BufferedWriter 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- dfs함수는 중위 순회를 진행하여 각 깊이의 최대 값과 최소값을 구합니다.
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
//트리 정보 클래스
static class node{
int left, right, parent; //왼쪽 자식, 오른쪽 자식, 부모 노드
node(int left, int right){
this.left = left;
this.right = right;
this.parent = -1;
}
}
static node[] tree; //트리 정보 저장하는 배열
static int[] minWidth, maxWidth; //각 깊이 최대, 최소 값 저장 배열
static int maxDepth = -1, index = 1; //최대 깊이
static int answerD = -1, answerW = -1; //최대 너비의 해당하는 레벨, 최대 너비
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedWriter
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
minWidth = new int[N+1];
maxWidth = new int[N+1];
tree = new node[N+1];
//배열 초기화
for(int i=0;i<=N;i++){
minWidth[i] = Integer.MAX_VALUE;
maxWidth[i] = Integer.MIN_VALUE;
tree[i] = new node(-1, -1);
}
StringTokenizer st;
//트리 정보 저장
for(int i=0;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
tree[a].left = b;
tree[a].right = c;
if(tree[a].left != -1)
tree[b].parent = a;
if(tree[a].right != -1)
tree[c].parent = a;
}
//중위 순회 진행하여 각 깊이 최대, 최소 값 구하기
for(int i=1;i<=N;i++){
//Root노드일 때 순회 시작
if(tree[i].parent == -1){
dfs(i, 1);
break;
}
}
//각 깊이 탐색하여 최대 너비 구하기
for(int i=1;i<=maxDepth;i++){
if(answerW < maxWidth[i] - minWidth[i] + 1){
answerW = maxWidth[i] - minWidth[i] + 1;
answerD = i;
}
}
//최대 너비와 그에 해당하는 레벨 BufferedWriter 저장
bw.write(answerD + " " + answerW);
bw.flush(); //결과 출력
bw.close();
br.close();
}
//중위 탐색 진행하는 함수
static void dfs(int cur, int d){
node n = tree[cur];
maxDepth = Math.max(maxDepth, d);
//Left
if(n.left != -1)
dfs(n.left, d+1);
//Root
minWidth[d] = Math.min(minWidth[d], index);
maxWidth[d] = Math.max(maxWidth[d], index++);
//Right
if(n.right != -1)
dfs(n.right, d+1);
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(문자열,JAVA)1120번, 문자열 (0) | 2022.10.06 |
|---|---|
| [백준] 알고리즘 분류(트리,JAVA)1761번, 정점들의 거리 (0) | 2022.10.02 |
| [백준] 알고리즘 분류(문자열,JAVA)9086번, 문자열 (0) | 2022.10.01 |
| [백준] 알고리즘 분류(트리,JAVA)11438번, LCA 2 (0) | 2022.09.30 |
| [백준] 알고리즘 분류(문자열,JAVA)1357번, 뒤집힌 덧셈 (0) | 2022.09.28 |




댓글