문제 링크
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명



접근 방법
이 문제에 핵심
1. 문제의 조건에서는 1 → 2 → 3 → 4사분면 순으로 'Z'모양의 탐색을 진행합니다.
2. (r, c)에 몇 번째 방문하는지 결과로 출력합니다.
알고리즘 진행 순서.
1. 입력된 정보를 저장합니다.
2. 재귀를 통해서 4개로 나뉘는 사분면을 탐색합니다.
3. 재귀 종료 후 얻은 (r, c)에 도착하는 수를 결과로 출력합니다.
사분면 탐색

1사분면의 조건 : r < 2ⁿ ÷ 2, c < 2ⁿ ÷ 2
2사분면의 조건 : r < 2ⁿ ÷ 2, c ≥ 2ⁿ ÷ 2 : 1사분면 방문
3사분면의 조건 : r ≥ 2ⁿ ÷ 2, c < 2ⁿ ÷ 2 : 1 , 2사분면 방문
4사분면의 조건 : r ≥ 2ⁿ ÷ 2, c ≥ 2ⁿ ÷ 2 : 1, 2, 3사분면 방문
2사분면부터 다른 사분면을 방문하고 해당 사분면을 방문하기 때문에 (2ⁿ ÷ 2)²의 배수만큼 더합니다.
예를 들어
(r, c)가 3사분면에 있으면 1사분면과 2사분면에 방문하기 때문에
(2ⁿ ÷ 2)² × 2을 방문한 뒤 해당 3사분면을 탐색합니다.
3사분면도 n이 1이 아닌 이상 4사분면으로 나뉘어지기 때문에 해당 재귀를 통해서 계속 나누어 가면 됩니다.
위 그림에서 4사분면에 값을 탐색하면 재귀를 통해 다시 4분면으로 나눌 수 있습니다.
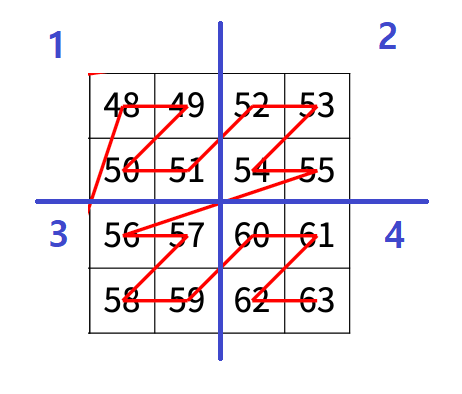
예제입력 1.
1. 입력된 정보를 저장합니다.
N : 2
r : 3
2. 재귀를 통해서 4개로 나뉘는 사분면을 탐색합니다.
재귀 시작!
N = 2

3사분면에 존재 : 1사분면, 2사분면 방문
방문한 횟수 : (2ⁿ ÷ 2)² × 2 = 4 × 2 = 8
N = 1

4사분면에 존재 : 1사분면, 2사분면, 3사분면 방문
방문한 횟수 : (2ⁿ ÷ 2)² × 2 = 1 × 3 = 3
(r, c) 방문!
3. 재귀 종료 후 얻은 (r, c)에 도착하는 수를 결과로 출력합니다.
8(N=2) + 3(N=1) = 11
11을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 이용하여 입력값을 띄어쓰기 기준 나누었습니다.
- search함수를 실행하여 사분면으로 나누는 재귀를 이용해 (r, c)방문 순서를 구합니다.
- (r, c)에 방문한 순서를 결과로 BufferedWriter에 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- search함수는 재귀를 통해 N이 1이 될 때까지 사분면으로 나눠서 탐색합니다.
결과코드
import java.util.*;
import java.io.*;
class Main {
public static void main(String args[]) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
//입력값 저장
int N = Integer.parseInt(st.nextToken());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
//현재 배열의 크기 구하기
int size = (int) Math.pow(2, N-1);
int answer = search(r, c, size); //재귀를 통한 사분면 탐색 진행
bw.write(answer + ""); //(r, c)에 방문 번호 BufferedWriter 저장
bw.flush(); //결과 출력
bw.close();
br.close();
}
//재귀를 통해 사분면 탐색
static int search(int r, int c, int size){
//N이 1일 때
if(size == 1){
//1, 2사분면일 때
if(r == 0)
return c;
else //3, 4사분면일 때
return c + 2;
}
int sum = 0;
if(r >= size){ //3, 4사분면일 때 1, 2사분면 지나기
sum += size * size * 2;
}
if(c >= size) //2, 4사분면일 때 1사분면이나 3사분면 방문
sum += size * size;
r %= size; //사분면에 맞게 r 변경
c %= size; //사분면에 맞게 c 변경
//다른 사분면 방문 정보 저장
sum += search(r, c, size/2);
return sum;
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(자료구조,JAVA)17219번, 비밀번호 찾기 (0) | 2023.01.19 |
|---|---|
| [백준] 알고리즘 분류(자료구조,JAVA)7662번, 이중 우선순위 큐 (0) | 2023.01.18 |
| [백준] 알고리즘 분류(트리,JAVA)16437번, 양 구출 작전 (0) | 2023.01.17 |
| [백준] 알고리즘 분류(구현,JAVA)19238번, 스타트 택시 (0) | 2023.01.15 |
| [백준] 알고리즘 분류(구현,JAVA)20056번, 마법사 상어와 파이어볼 (2) | 2023.01.14 |




댓글