문제 링크
1761번: 정점들의 거리
첫째 줄에 노드의 개수 N이 입력되고 다음 N-1개의 줄에 트리 상에 연결된 두 점과 거리를 입력받는다. 그 다음 줄에 M이 주어지고, 다음 M개의 줄에 거리를 알고 싶은 노드 쌍이 한 줄에 한 쌍씩
www.acmicpc.net
주의사항
- JAVA를 사용하여 프로그램을 사용하였습니다.
- 백준에서 코드를 작성하였을 때 아래 형태에서 Main에서 결과가 출력되어야 합니다.
public class Main{
public static void main(String[] args){
}
}문제 설명

접근 방법
이 문제에 핵심
1. 트리에 대한 정보가 주어지고 M개의 두 노드 사이의 거리를 결과로 출력합니다.
2. 정점은 1~N번까지 존재합니다.
이 문제를 풀기 전 아래 문제를 풀고 오는 것을 추천드립니다.
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
[백준] 알고리즘 분류(트리,JAVA)11438번, LCA 2
문제 링크 11438번: LCA 2 첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지
tussle.tistory.com
알고리즘 진행 순서.
1. 입력된 트리의 정보를 저장합니다.
2. 입력된 정보로 트리 형성 및 부모 노드(DP)와 깊이를 따로 저장합니다.
3. LCA로 최소 공통 조상 노드를 이용해서 M개의 두 노드의 거리를 결과로 출력합니다.
시도 과정
1. BFS를 이용하여 해결하려고 하였으나 시간초과가 발생.
2. LCA에서 이분탐색을 사용하지 않는 방법으로 이용하였지만 메모리 초과 발생.
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
[백준] 알고리즘 분류(트리,JAVA)11437번, LCA
문제 링크 11437번: LCA 첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고
tussle.tistory.com
3. LCA에서 이분탐색을 사용하는 방법으로 하였지만 메모리 초과 다시 발생.
4. 이분 탐색하는 LCA와 루트 노드에서 각 노드의 거리를 구한 뒤 점화식으로 결과를 구하였을 때 성공!
LCA.
※이분 탐색을 이용하여 LCA를 진행하는 것은 LCA2 문제를 풀고 오셨다고 생각하고 생략하겠습니다.
두 노드의 거리 구하기.
아래와 같은 트리가 존재할 때

루트 노드 1에서 거리를 표현하면
dis[2] = 3
dis[3] = 2
dis[4] = 7
dis[5] = 5
dis[6] = 3
만약 거리를 구하는 노드가 (4, 5)으로 입력받으면
정점 4와 정점 5의 최소 공통 조상 노드에서 각 정점의 거리의 합입니다.
점화식을 구해보면
dis[4] = 1 → 2 → 4의 거리의 합
dis[5] = 1 → 2 → 5의 거리의 합
4와 5의 최소 공통 조상 노드 : 2
최소 공통 조상 노드에서 각 정점 거리의 합
(2 → 4) + (2 → 5)입니다.
dis[4] + dis[5] = (1 → 2) + (2 → 4) + (1 → 2) + (2 → 5)
dis[4] + dis[5] - ((1 → 2) × 2) = (2 → 4) + (2 → 5)
위에 식으로 구할 수 있는 점화식은
두 정점이 n, m이고 최소 공통 조상 노드가 k일 때
거리를 구하는 식은
점화식 : dis[n] + dis[m] - (dis[k] × 2)
4와 5를 적용시켜보면
dis[4] + dis[5] - (dis[2] × 2) = 7 + 5 - 6 = 6
예제입력 1.
1. 입력된 트리의 정보를 저장합니다.
※루트 노드를 1번으로 하는 이유는 모든 테스트에 항상 존재하기 때문입니다.
N : 7
(1 ↔ 6), 13
(6 ↔ 3), 9
(3 ↔ 5), 7
(4 ↔ 1), 3
(2 ↔ 4), 20
(4 ↔ 7), 2
M : 3
(1, 6), (1, 4), (2, 6)
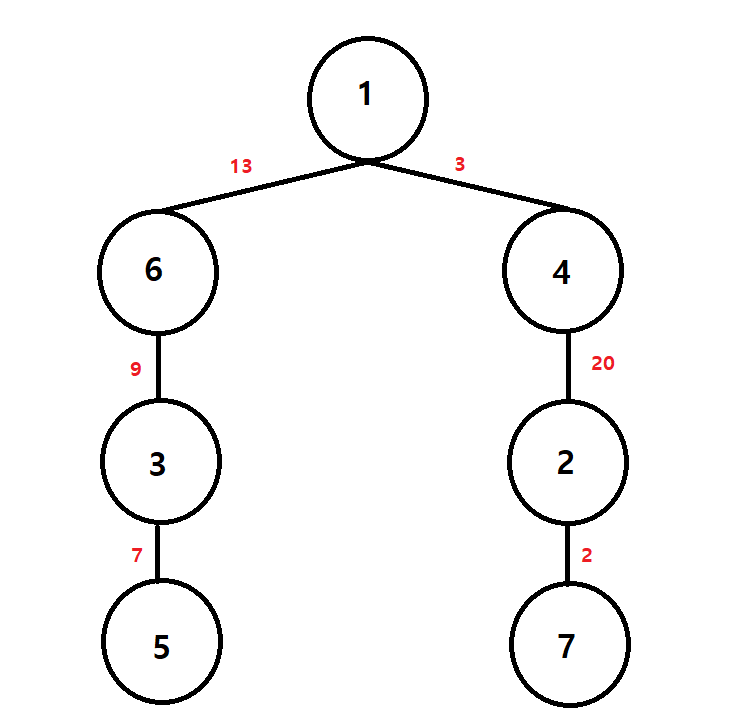
2. 입력된 정보로 트리 형성 및 부모 노드(DP)와 깊이, 거리를 따로 저장합니다.
부모 노드의 parent[m][0](1칸 위에 있는 부모 노드)를 저장하였습니다.
parent[5][0] = 3, parent[3][0] = 6
.....
노드의 깊이도 배열로 따로 저장하였습니다.
depth[5] = 4, depth[3] = 3
.....
루트 노드에서 각 노드의 거리도 배열로 따로 저장하였습니다.
width[5] = 29, width[3] = 22
.....
점화식을 이용하여 parent[][]를 구성합니다.
parent[5][1] = parent[parent[5][0]][0] = parent[3][0] = 6
parent[2][1] = parent[parent[2][0]][0] = parent[4][0] = 1
....
3. LCA로 최소 공통 조상 노드를 이용해서 M개의 두 노드의 거리를 결과로 출력합니다.
(1, 6)의 최소 공통 조상 노드 : 1
dis[1] + dis[6] - (dis[1] × 2) = 0 + 13 - 0 = 13
(1, 4)의 최소 공통 조상 노드 : 1
dis[1] + dis[4] - (dis[1] × 2) = 0 + 3 - 0 = 3
(2, 6)의 최소 공통 조상 노드 : 1
dis[2] + dis[6] - (dis[1] × 2) = 23 + 13 - 0 = 36
13, 3, 36을 결과로 출력합니다.
- BufferedReader를 사용하여 입력되는 정보를 저장합니다.
- StringTokenizer를 통해서 트리의 정보를 띄어쓰기 기준 나누었습니다.
- getMaxDepth를 실행하여 트리의 최대 깊이를 구하였습니다.
- setTree와 fillParent를 실행하여 트리의 정보들을 설정하였습니다.
- M개의 두 노드를 LCA함수와 점화식을 이용하여 얻은 결과를 BufferedWriter 저장하였습니다.
- BufferedWriter에 저장된 결과값을 출력하였습니다.
- getMaxDepth함수는 N에 따른 트리의 최대 깊이를 구합니다.
- setTree함수는 입력받은 정보로 깊이, 루트 노드에서의 거리 등을 설정합니다.
- fillParent는 점화식을 이용해서 parent[][]배열을 구성합니다.
- LCA는 이분 탐색을 통해서 최소 공통 조상 노드를 구합니다.
import java.io.*;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.StringTokenizer;
public class Main {
//트리 노드 관련 정보 클래스
static class node{
int next, width;
public node(int next, int width){
this.next = next;
this.width = width;
}
}
static int N,M, maxDepth = -1;
static ArrayList<ArrayList<node>> tree = new ArrayList<>(); //트리 정보 저장 리스트
static int[] depth, width; //정점 깊이, 루트 정점에서의 거리 저장 배열
static int[][] parent; //각 부모 노드의 메모이제이션
public static void main(String[] args) throws IOException{
//입력값 처리하는 BufferedReader
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//결과값 출력하는 BufferedWriter
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
getMaxDepth();
parent = new int[N+1][maxDepth+1];
width = new int[N+1];
depth = new int[N+1];
for(int i=0;i<=N;i++)
tree.add(new ArrayList<>());
//트리의 정보 저장
for(int i=1;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
tree.get(a).add(new node(b, w));
tree.get(b).add(new node(a, w));
}
setTree(1, 1, 0, 0); //트리의 형태 설정
fillParent(); //점화식을 통한 부모 노드 설정
M = Integer.parseInt(br.readLine());
//M개의 두 노드의 거리 BufferedWriter 저장
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
//점화식
int result = width[a] + width[b] - (width[LCA(a, b)] * 2);
bw.write(result+ "\n"); //BufferedWriter 저장
}
bw.flush(); //결과 출력
bw.close();
br.close();
}
//최대 깊이 구하는 함수
static void getMaxDepth(){
maxDepth = (int)Math.ceil(Math.log(N) / Math.log(2)) + 1;
}
//트리 형태로 깊이와 루트 노드에서의 거리 저장 함수
static void setTree(int c, int d, int p, int w){
depth[c] = d;
width[c] = w;
for(node next : tree.get(c)){
if(next.next == p)
continue;
parent[next.next][0] = c;
setTree(next.next, d+1, c, w + next.width);
}
}
//점화식으로 부모 노드 관련 배열 설정하는 함수
static void fillParent(){
for(int i=1;i<=maxDepth;i++){
for(int j=1;j<=N;j++){
parent[j][i] = parent[parent[j][i-1]][i-1];
}
}
}
//이분 탐색으로 최소 공통 조상 노드 구하는 함수
static int LCA(int a, int b){
int ah = depth[a];
int bh = depth[b];
//항상 ah > bh가 되도록 설정
if(ah < bh){
int temp = b;
b = a;
a = temp;
}
//깊이 동일하게 맞추기
for(int i=maxDepth-1;i>=0;i--){
if(Math.pow(2, i) <= depth[a] - depth[b]){
a = parent[a][i];
}
}
//a와 b가 동일하면 탐색하지 않아도 가능
if(a == b)
return a;
//동시에 같이 올라가기
for(int i=maxDepth-1;i>=0;i--){
if(parent[a][i]!=parent[b][i]){
a = parent[a][i];
b = parent[b][i];
}
}
return parent[a][0]; //최소 공통 조상 노드 반환
}
}'백준' 카테고리의 다른 글
| [백준] 알고리즘 분류(트리,JAVA)14725번, 개미굴 (0) | 2022.10.06 |
|---|---|
| [백준] 알고리즘 분류(문자열,JAVA)1120번, 문자열 (0) | 2022.10.06 |
| [백준] 알고리즘 분류(트리,JAVA)2250번, 트리의 높이와 너비 (0) | 2022.10.02 |
| [백준] 알고리즘 분류(문자열,JAVA)9086번, 문자열 (0) | 2022.10.01 |
| [백준] 알고리즘 분류(트리,JAVA)11438번, LCA 2 (0) | 2022.09.30 |




댓글